
已知函数 为奇函数,且对定义域内的任意x都有
为奇函数,且对定义域内的任意x都有 .当
.当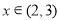 时,
时, ,给出以下4个结论:①函数
,给出以下4个结论:①函数 的图象关于点(k,0)(k
的图象关于点(k,0)(k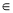 Z)成中心对称;②函数
Z)成中心对称;②函数 是以2为周期的周期函数;③当
是以2为周期的周期函数;③当 时,
时, ;④函数
;④函数 在(k,k+1)(k
在(k,k+1)(k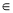 Z)上单调递增,则结论正确的序号是.
Z)上单调递增,则结论正确的序号是.
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练二(解析版) 题型:选择题
已知一空间几何体的三视图如图所示,则该几何体的体积为( )

A. π cm3 B.3π cm3 C.
π cm3 B.3π cm3 C. π cm3 D.
π cm3 D. π cm3
π cm3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省张掖市高三第三次诊断考试理科数学试卷(解析版) 题型:解答题
已知 .
.
(1)求函数 在
在 上的最小值;
上的最小值;
(2)对一切 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)证明:对一切 ,都有
,都有 成立.
成立.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省张掖市高三第三次诊断考试理科数学试卷(解析版) 题型:选择题
在等差数列 中,
中, =
= ,则数列
,则数列 的前11项和
的前11项和 =( ).
=( ).
A.24 B.48 C.66 D.132
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省张掖市高三第三次诊断考试文科数学试卷(解析版) 题型:解答题
已知函数 ,其中a为常数.
,其中a为常数.
(1)当 时,求
时,求 的最大值;
的最大值;
(2)若 在区间(0,e]上的最大值为
在区间(0,e]上的最大值为 ,求a的值;
,求a的值;
(3)当 时,试推断方程
时,试推断方程 =
=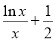 是否有实数解.
是否有实数解.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省张掖市高三第三次诊断考试文科数学试卷(解析版) 题型:选择题
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积 为( ).
为( ).

A. B.
B.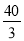 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省张掖市高三第三次诊断考试文科数学试卷(解析版) 题型:选择题
在等差数列 中,
中, =
= ,则数列
,则数列 的前11项和
的前11项和 =( ).
=( ).
A.24 B.48 C.66 D.132
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省高三十三校联考第二次考试理科数学试卷(解析版) 题型:选择题
若实数a,b,c成等差数列,点 在动直线
在动直线 上的射影为
上的射影为 ,点
,点 ,则
,则 的最大值是( )
的最大值是( )
A. B.
B.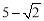 C.
C.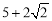 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com