
 的首项
的首项 .
. 为等比数列;
为等比数列; ,若
,若 ,求最大正整数
,求最大正整数 的值;
的值; ,使
,使 成等差数列,且
成等差数列,且 成等比数列?如果存在,请给予证明;如果不存在,请说明理由.
成等比数列?如果存在,请给予证明;如果不存在,请说明理由.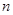 的值为100;(3)满足题意的正整数
的值为100;(3)满足题意的正整数 不存在.
不存在.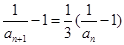 ,据等比数列的定义知数列
,据等比数列的定义知数列 为等比数列;(2)由等比数列
为等比数列;(2)由等比数列 的通项公式求出
的通项公式求出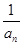 的通项公式.易得出
的通项公式.易得出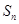 ,再解出
,再解出 即可;(3)假设存在,可得
即可;(3)假设存在,可得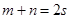 ,
,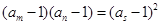 由通项公式代入化简可得
由通项公式代入化简可得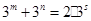 ,因为
,因为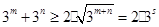 ,当且仅当
,当且仅当 时等号成立,又
时等号成立,又 互不相等,则不存在.
互不相等,则不存在. ,所以
,所以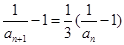
 ,所以
,所以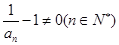 ,所以数列
,所以数列 为等比数列. 4分
为等比数列. 4分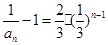 ,所以
,所以 ,
,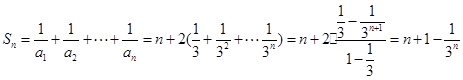 ,
, ,则
,则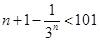 ,所求最大正整数
,所求最大正整数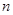 的值为100. 9分
的值为100. 9分 ,
,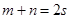 ,
,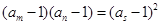 ,
,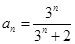 ,所以
,所以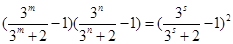 ,
,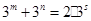 ,因为
,因为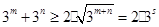 ,
, 时等号成立,又
时等号成立,又 互不相等,
互不相等, 不存在. 14分
不存在. 14分

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com