
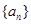 为正项递增数列,且
为正项递增数列,且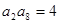 ,
,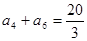 ,数列
,数列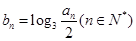 .
.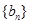 的通项公式;
的通项公式;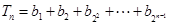 ,求
,求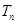 .
.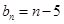 ;(2)
;(2) .
.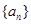 的通项
的通项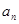 ,根据题设条件可采取基本量法,也可应用等比数列的性质,如
,根据题设条件可采取基本量法,也可应用等比数列的性质,如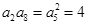 ,
,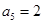 ,
,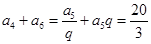 ,可解得
,可解得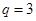 或
或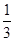 ,数列
,数列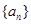 又是递增的数列,这样取
又是递增的数列,这样取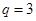 ,由此可得
,由此可得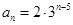 ,于是有
,于是有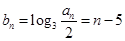 ;(2)要求
;(2)要求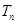 ,我们应该确定它是哪个数列的前
,我们应该确定它是哪个数列的前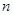 项和,从已知可能看出,可设
项和,从已知可能看出,可设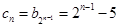 ,因此求
,因此求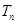 时可用分组求和的方法,化为一个等比数列的和与一个常数列的和,即
时可用分组求和的方法,化为一个等比数列的和与一个常数列的和,即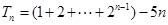 .
.
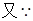
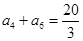
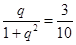 . 2分
. 2分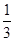 ,
,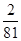 . 4分
. 4分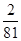 ·3n-1=2·3n-5.∴bn=log3
·3n-1=2·3n-5.∴bn=log3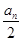 =n-5. 6分
=n-5. 6分 =(1-5)+(2-5)+(22-5)+ +(2n-1-5)
=(1-5)+(2-5)+(22-5)+ +(2n-1-5)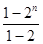 -5n=
-5n=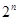 -5n-1 12分(三步,每步2分)
-5n-1 12分(三步,每步2分)

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
 的首项
的首项 .
. 为等比数列;
为等比数列; ,若
,若 ,求最大正整数
,求最大正整数 的值;
的值; ,使
,使 成等差数列,且
成等差数列,且 成等比数列?如果存在,请给予证明;如果不存在,请说明理由.
成等比数列?如果存在,请给予证明;如果不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com