
(本题满分10分)已知函数 ,(
,(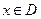 ),若同时满足以下条件:
),若同时满足以下条件:
① 在D上单调递减或单调递增
在D上单调递减或单调递增
② 存在区间[ ]
]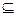 D,使
D,使 在[
在[ ]上的值域是[
]上的值域是[ ],那么称
],那么称 (
(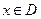 )为闭函数。
)为闭函数。
(1)求闭函数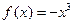 符合条件②的区间[
符合条件②的区间[ ];
];
(2)判断函数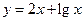 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[ ];若不是请说明理由;
];若不是请说明理由;
(3)若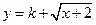 是闭函数,求实数
是闭函数,求实数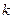 的取值范围.
的取值范围.
 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:解答题
在边长为60cm的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?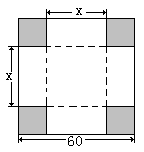
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某皮制厂去年生产皮质小包的年产量为10万件,每件皮质小包的销售价格平均为100元,生产成本为80元.从今年起工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本,预计产量每年递增1万件.设第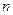 年每件小包的生产成本
年每件小包的生产成本 元,若皮制产品的销售价格不变,第
元,若皮制产品的销售价格不变,第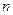 年的年利润为
年的年利润为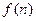 万元(今年为第一年).
万元(今年为第一年).
(Ⅰ)求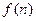 的表达式
的表达式
(Ⅱ)问从今年算起第几年的利润最高?最高利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: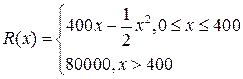 ,其中
,其中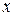 是仪器的月产量.
是仪器的月产量.
(1) 将利润表示为月产量的函数 ;
;
(2) 当月产量为何值时,公司所获利润最大?最大利润为多少元(总收益=总成本+利润) ?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本题满分12分)
一批救灾物资随26辆汽车从某市以x km/h的速度匀速开往相距400 km的灾区.为安全起见,每两辆汽车的前后间距不得小于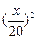 km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时
km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时 间,问运输时间最少需要多少小时?
间,问运输时间最少需要多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)设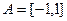 ,
,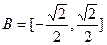 ,函数
,函数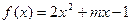 ,
,
(Ⅰ)设不等式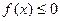 的解集为C,当
的解集为C,当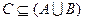 时,求实数
时,求实数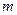 取值范围;
取值范围;
(Ⅱ)若对任意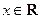 ,都有
,都有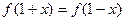 成立,试求
成立,试求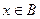 时,
时, 的值
的值 域;
域;
(Ⅲ)设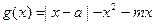
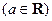 ,求
,求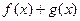 的最
的最 小值.
小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com