(本题满分12分)某皮制厂去年生产皮质小包的年产量为10万件，每件皮质小包的销售价格平均为100元，生产成本为80元.从今年起工厂投入100万元科技成本，并计划以后每年比上一年多投入100万元科技成本，预计产量每年递增1万件.设第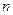
年每件小包的生产成本
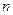元，若皮制产品的销售价格不变，第年的年利润为
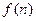万元（今年为第一年）.
（Ⅰ）求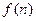的表达式
（Ⅱ）问从今年算起第几年的利润最高？最高利润为多少万元？
培优好卷单元加期末卷系列答案科目：高中数学 来源： 题型：解答题
（本题满分10分）已知函数
,(
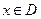)，若同时满足以下条件：
①在D上单调递减或单调递增
② 存在区间[
]
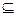D,使在[]上的值域是[]，那么称(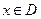)为闭函数。
（1）求闭函数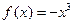
符合条件②的区间[]；
（2）判断函数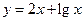
是不是闭函数？若是请找出区间[]；若不是请说明理由；
（3）若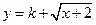
是闭函数，求实数
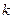的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
本题满分12分，每小题各4分）
已知函数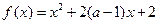
，
（1）若函数
的值域为
，求实数a的值；
（2）若函数的递增区间为，求实数a的值；
（3）若函数在区间
上是增函数，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt∆FHE,H是直角顶点)来处理污水,管道越长，污水净化效果越好.设计要求管道的接口H是AB的中点，E,F分别落在线段BC,AD上.已知AB=20米，AD=10
米，记∠BHE=θ.
（1）试将污水净化管道的长度L表示为θ的函数,并写出定义域；
（2）若sinθ+cosθ=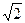
，求此时管道的长度L；
（3）问：当θ取何值时，污水净化效果最好？
并求出此时管道的长度.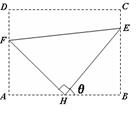
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
医学上为了研究传染病在传播的过程中病毒细胞的生长规律及其预防措施，将
个病毒细胞注入到一只小白鼠的体内进行试验．在试验过程中，得到病毒细胞的数量与时间的关系记录如下表：
| 时间（小时） | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 病毒细胞总数（个） | | 2 | 4 | 8 | 16 | 32 | 64 |
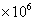个时，小白鼠将死亡，但有一种药物对杀死此种病毒有一定效果，用药后，即可杀死其体内的大部分病毒细胞．
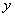与时间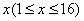
的函数关系式；
）查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
……6分
，令
，故
时，
不符合实际意义， ……………………………10分
时，
的图像，并指出它的单调区间.
.
的奇偶性，并证明；
对任意的
，都有
成立，且当
时，
。
为奇函数； （2）求证：
是R上的增函数；
，解不等式
．
（其中
为常量且
）的图像经过点
.
在
时恒成立，求实数
的取值范围.