
如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt∆FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=10 米,记∠BHE=θ.
米,记∠BHE=θ.
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)若sinθ+cosθ=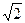 ,求此时管道的长度L;
,求此时管道的长度L;
(3)问:当θ取何值时,污水净化效果最好?
并求出此时管道的长度.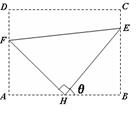
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分)某皮制厂去年生产皮质小包的年产量为10万件,每件皮质小包的销售价格平均为100元,生产成本为80元.从今年起工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本,预计产量每年递增1万件.设第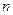 年每件小包的生产成本
年每件小包的生产成本 元,若皮制产品的销售价格不变,第
元,若皮制产品的销售价格不变,第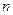 年的年利润为
年的年利润为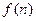 万元(今年为第一年).
万元(今年为第一年).
(Ⅰ)求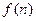 的表达式
的表达式
(Ⅱ)问从今年算起第几年的利润最高?最高利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本题满分12分)
一批救灾物资随26辆汽车从某市以x km/h的速度匀速开往相距400 km的灾区.为安全起见,每两辆汽车的前后间距不得小于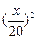 km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时
km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时 间,问运输时间最少需要多少小时?
间,问运输时间最少需要多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知:函数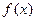 对一切实数
对一切实数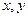 都有
都有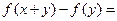
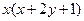 成立,且
成立,且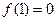 .
.
(1)求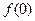 的值。
的值。
(2)求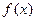 的解析式。
的解析式。
(3)已知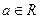 ,设P:当
,设P:当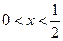 时,不等式
时,不等式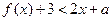 恒成立;Q:当
恒成立;Q:当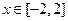 时,
时,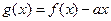 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的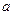 的集合记为
的集合记为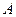 ,满足Q成立的
,满足Q成立的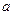 的集合记为
的集合记为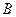 ,求
,求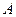 ∩
∩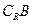 (
(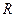 为全集)。
为全集)。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)设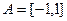 ,
,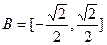 ,函数
,函数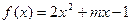 ,
,
(Ⅰ)设不等式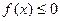 的解集为C,当
的解集为C,当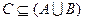 时,求实数
时,求实数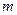 取值范围;
取值范围;
(Ⅱ)若对任意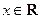 ,都有
,都有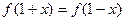 成立,试求
成立,试求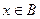 时,
时, 的值
的值 域;
域;
(Ⅲ)设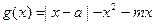
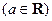 ,求
,求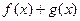 的最
的最 小值.
小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)已知二次函数 对
对 都满足
都满足 且
且 ,设函数
,设函数
( ,
, ).
).
(1)求 的表达式;
的表达式;
(2)若 ,使
,使
 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(3)设 ,
, ,求证:对于
,求证:对于 ,恒有
,恒有 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com