
已知函数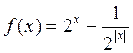
(1)若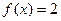 ,求
,求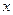 的值;
的值;
(2)若对任意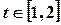 ,
,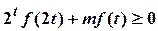 恒成立,求实数
恒成立,求实数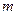 的取值范围。
的取值范围。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
.(12分)已知函数 的定义域为
的定义域为 ,且同时满足:(Ⅰ)对任意
,且同时满足:(Ⅰ)对任意 ,总有
,总有 ;(Ⅱ)
;(Ⅱ)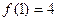 ;(Ⅲ)若
;(Ⅲ)若 ,则有
,则有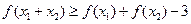
(1)试求 的值;
的值;
(2)试求函数 的最大值;
的最大值;
(3)试证明:当 时,
时, 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知p:方程x2+mx+1=0有两个不等的 负实根,q:方程4x2+4(m-2)x+1=0无实根。若p或q为真,p且q为假。求实数m的取值范围。
负实根,q:方程4x2+4(m-2)x+1=0无实根。若p或q为真,p且q为假。求实数m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt∆FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=10 米,记∠BHE=θ.
米,记∠BHE=θ.
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)若sinθ+cosθ=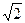 ,求此时管道的长度L;
,求此时管道的长度L;
(3)问:当θ取何值时,污水净化效果最好?
并求出此时管道的长度.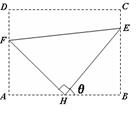
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业 甲将经营状态良好的某种消费品专卖店以58万元的优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息).已知经营该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)与售价p(元/件)的关系如图.
甲将经营状态良好的某种消费品专卖店以58万元的优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息).已知经营该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)与售价p(元/件)的关系如图.
(1)写出销量q与售价p的函数关系式;
(2)当售价p定为多少时,月利润最多?
(3)企业乙最早可望在经营该专卖店几个月后还清转让费?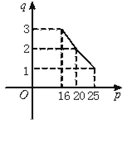
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com