
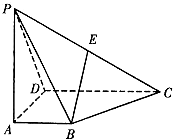
 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.分析 (1)设PA=b,建立如图所示空间直角坐标系,证明$\overrightarrow{AB}•\overrightarrow{BE}$=0,即可证明直线BE∥平面PAD;
(2)①若直线BE⊥平面PCD,$\overrightarrow{BE}•\overrightarrow{PC}$=0,即可求PA的长;
②利用向量的夹角公式,即可求异面直线PD与BC所成角的余弦值.
解答 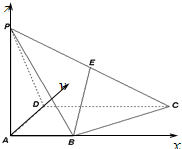 (1)证明:设PA=b,建立如图所示空间直角坐标系,A(0,0,0),B(1,0,0),P(0,0,b),D(0,2,0),C(2,2,0),E(1,1,$\frac{b}{2}$).…(2分)
(1)证明:设PA=b,建立如图所示空间直角坐标系,A(0,0,0),B(1,0,0),P(0,0,b),D(0,2,0),C(2,2,0),E(1,1,$\frac{b}{2}$).…(2分)
$\overrightarrow{BE}$=(0,1,$\frac{b}{2}$),平面PAD的法向量为$\overrightarrow{AB}$=(1,0,0),
∴$\overrightarrow{AB}•\overrightarrow{BE}$=0,…(5分)
又BE?平面PAD,
∴直线BE∥平面PAD.…(7分)
(2)解:①∵直线BE⊥平面PCD,
∴BE⊥PC,即$\overrightarrow{BE}•\overrightarrow{PC}$=0.…(8分)
又$\overrightarrow{PC}$=(2,2,-b),
∴$\overrightarrow{BE}•\overrightarrow{PC}$=2-$\frac{{b}^{2}}{2}$=0,…(9分)
即b=2,∴PA的长为2.…(10分)
②$\overrightarrow{PD}$=(0,2,-2),$\overrightarrow{BC}$=(1,2,0),…(11分)
∴cos<$\overrightarrow{PD}$,$\overrightarrow{BC}$>=$\frac{4}{2\sqrt{2}•\sqrt{5}}$=$\frac{\sqrt{10}}{5}$,…(13分)
∴异面直线PD与BC所成角的余弦值为$\frac{\sqrt{10}}{5}$.…(14分)
点评 本题考查线面平行的判定,考查异面直线PD与BC所成角的余弦值,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{e^2}{4}$,+∞) | B. | ($\frac{{{e^{\;}}}}{2}$,+∞) | C. | (1,$\frac{e^2}{4}$) | D. | (1,$\frac{{{e^{\;}}}}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)一定存在极大值和极小值 | |
| B. | 若函数f(x)在(-∞,x1),(x2,+∞)上是增函数,则x2-x1≥$\frac{2\sqrt{3}}{3}$ | |
| C. | 函数f(x)的图象是中心对称图形 | |
| D. | 函数f(x)的图象在点(x0,f(x0))(x0∈R)处的切线与f(x)的图象必有两个不同的公共点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com