
分析 (1)通过bn+1=1-$\frac{1}{{b}_{n}}$、b${\;}_{1}=\frac{1}{2}$,直接代入计算即可;
(2)通过bn+1=1-$\frac{1}{{b}_{n}}$计算可知bn+1=$\frac{{b}_{n}-1}{{b}_{n}}$,bn+2=-$\frac{1}{{b}_{n}-1}$,bn+3=bn;
(3)通过(2)可知b3n+1=b1=$\frac{1}{2}$,b3n+2=b2=-1,b3n+3=b3=2,并项相加即得结论.
解答 (1)解:因为bn+1=1-$\frac{1}{{b}_{n}}$,b${\;}_{1}=\frac{1}{2}$,
所以${b}_{2}=1-\frac{1}{{b}_{1}}$=-1,${b}_{3}=1-\frac{1}{{b}_{2}}=2$,${b}_{4}=1-\frac{1}{{b}_{3}}$=$\frac{1}{2}$;
(2)证明:因为bn+1=1-$\frac{1}{{b}_{n}}$=$\frac{{b}_{n}-1}{{b}_{n}}$,
所以bn+2=1-$\frac{1}{{b}_{n+1}}$=1-$\frac{{b}_{n}}{{b}_{n}-1}$=-$\frac{1}{{b}_{n}-1}$,
${b}_{n+3}=1-\frac{1}{{b}_{n+2}}$=1-$\frac{1}{-\frac{1}{{b}_{n}-1}}$=bn,
所以bn+3=bn;
(3)解:由(2)可知b3n+1=b1=$\frac{1}{2}$,b3n+2=b2=-1,b3n+3=b3=2,
所以S2012=(b1+b2+b3)+(b4+b5+b6)+…+(b2008+b2009+b2010)+b2011+b2012
=670×($\frac{1}{2}$-1+2)+$\frac{1}{2}$-1
=$\frac{2009}{2}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
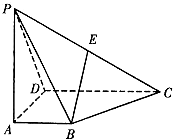 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
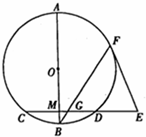 如图,AB是圆O的直径,弦CD⊥AB于点M,E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于G.
如图,AB是圆O的直径,弦CD⊥AB于点M,E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (1,0) | C. | (0,-1) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com