
分析 通过设M到直线l的距离为d、记右焦点为F′,根据椭圆的第二定义得|MF′|=$\frac{c}{a}$•d,利用椭圆定义可知$\frac{3}{2}$d=2a-$\frac{c}{a}$•d,从而d=$\frac{4{a}^{2}}{3a+2c}$,利用|MF|∈(a-c,a+c),进而计算即得结论.
解答 解:设M到直线l的距离为d,记右焦点为F′,
根据椭圆的第二定义得$\frac{|MF′|}{d}$=e=$\frac{c}{a}$,
∵|MF|+|MF′|=2a,
∴|MF|=2a-|MF′|=2a-$\frac{c}{a}$•d,
又∵|MF|=$\frac{3}{2}$d,
∴$\frac{3}{2}$d=2a-$\frac{c}{a}$•d,即d=$\frac{4{a}^{2}}{3a+2c}$,
∴$\frac{3}{2}$d=$\frac{6{a}^{2}}{3a+2c}$,
又∵|MF|∈(a-c,a+c),
∴a-c≤$\frac{6{a}^{2}}{3a+2c}$≤a+c,
整理得:2$(\frac{c}{a})^{2}$+$\frac{c}{a}$+3≥0,且2$(\frac{c}{a})^{2}$+5$\frac{c}{a}$-3≥0,
解得:$\frac{c}{a}$≥$\frac{1}{2}$或$\frac{c}{a}$≤-3(舍),
又∵$\frac{c}{a}$<1,
∴$\frac{1}{2}$≤$\frac{c}{a}$<1,即椭圆离心率的取值范围是[$\frac{1}{2}$,1),
故答案为:[$\frac{1}{2}$,1).
点评 本题主要考查了椭圆的基本性质,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 20 | C. | 25 | D. | 39 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
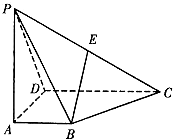 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com