
【题目】在△ABC中,角A,B,C的对边分别为a,b,c, ![]() asinB+bcosA=c. (Ⅰ)求B;
asinB+bcosA=c. (Ⅰ)求B;
(Ⅱ)若a=2 ![]() c,S△ABC=2
c,S△ABC=2 ![]() ,求b.
,求b.
【答案】解:(Ⅰ)由题意得, ![]() asinB+bcosA=c, 由正弦定理得
asinB+bcosA=c, 由正弦定理得 ![]() sinAsinB+sinBcosA=sinC
sinAsinB+sinBcosA=sinC
所以 ![]() sinAsinB+sinBcosA=sin(A+B),
sinAsinB+sinBcosA=sin(A+B),
即 ![]() sinAsinB=sinAcosB,
sinAsinB=sinAcosB,
由sinA≠0得, ![]() sinB=cosB,则tanB=
sinB=cosB,则tanB= ![]() ,
,
又0<B<π,所以B=30°.
(Ⅱ)由(Ⅰ)和a=2 ![]() c得,
c得,
S△ABC= ![]() acsinB=
acsinB= ![]() c2=2
c2=2 ![]() ,解得c=2,a=4
,解得c=2,a=4 ![]() .
.
由余弦定理得b2=a2+c2﹣ ![]() ac=28,
ac=28,
所以b=2 ![]()
【解析】(Ⅰ)由正弦定理化简已知的式子,由内角的范围和特殊角的三角函数值求出B;(Ⅱ)根据条件和三角形的面积公式求出c、a,再由余弦定理求出b.
【考点精析】本题主要考查了正弦定理的定义和余弦定理的定义的相关知识点,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知直线l1:3x+2y﹣1=0和l2:5x+2y+1=0的交点为A
(1)若直线l3:(a2﹣1)x+ay﹣1=0与l1平行,求实数a的值;
(2)求经过点A,且在两坐标轴上截距相等的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处. 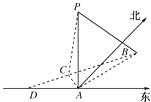
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上的点到两个焦点的距离之和为
上的点到两个焦点的距离之和为![]() ,短轴长为
,短轴长为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相切,探究
相切,探究![]() 是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内一动点![]() 与两定点
与两定点![]() 和
和![]() 连线的斜率之积等于
连线的斜率之积等于![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设直线![]() :
: ![]() (
(![]() )与轨迹
)与轨迹![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,当
,当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).


(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com