
已知函数![]()
(1)若定义域为R,求a范围
(2)若值域为R,求a范围.
考点:
函数的定义域及其求法;函数的值域.
专题:
函数的性质及应用.
分析:
(1)根据函数![]() 的定义域为R,说明对任意实数x,对数式的真数恒大于0,而真数是二次三项式,由其对应的二次方程的判别式小于0即可求得a的取值范围,同时兼顾对数式的底数有意义;
的定义域为R,说明对任意实数x,对数式的真数恒大于0,而真数是二次三项式,由其对应的二次方程的判别式小于0即可求得a的取值范围,同时兼顾对数式的底数有意义;
(2)根据函数![]() 的值域为R,说明对数式的真数能取到大于0的所有实数,则真数上的二次三项式对应的抛物线顶点应在x轴上或其下方,故其对应的二次方程的判别式应大于等于0,由此求解a的取值范围.
的值域为R,说明对数式的真数能取到大于0的所有实数,则真数上的二次三项式对应的抛物线顶点应在x轴上或其下方,故其对应的二次方程的判别式应大于等于0,由此求解a的取值范围.
解答:
解:(1)由函数![]() 的定义域为R,
的定义域为R,
说明x2+ax+2>0对任意实数恒成立,
则不等式x2+ax+2>0对应二次方程的△=a2﹣8<0,即![]() .
.
又a>0且a≠1,所以,0<a<![]() ,且a≠1.
,且a≠1.
故使函数![]() 的定义域为R的a的取值范围是(0,1)∪(1,
的定义域为R的a的取值范围是(0,1)∪(1,![]() );
);
(2)函数![]() 的值域为R,
的值域为R,
说明x2+ax+2能取到大于0的所有实数,
则不等式x2+ax+2>0对应二次方程的△=a2﹣8≥0,解得:![]() 或
或![]() .
.
又a>0且a≠1,所以,使函数![]() 的值域为R的a的取值范围是(2
的值域为R的a的取值范围是(2![]() ,+∞).
,+∞).
点评:
本题考查了函数的定义域,函数的值域,考查了数学转化思想,解答此题的关键是由函数值域是R,得到真数的二次三项式的判别式大于等于0,是基础题,解答时易忽略底数的限制条件,也是易错题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
 已知函数f(x)=2x+
已知函数f(x)=2x+| 5 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年大连市一模文)(14分) 已知函数![]() 在[1,2]上的最小值为
在[1,2]上的最小值为![]() 是函数
是函数![]() 图象上不同两点,且线段P1P2的中点P的横坐标为
图象上不同两点,且线段P1P2的中点P的横坐标为![]()
(I)求t的值;
(II)求证:点P的纵坐标是定值;
(III)若数列![]() 的前m项和Sm.
的前m项和Sm.
查看答案和解析>>
科目:高中数学 来源:2014届广东省广州市越秀区高三上学期摸底考试文科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)试问 的值是否为定值?若是,求出该定值;若不是,请说明理由;
的值是否为定值?若是,求出该定值;若不是,请说明理由;
(2)定义 ,其中
,其中 ,求
,求 ;
;
(3)在(2)的条件下,令 .若不等式
.若不等式 对
对 且
且 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
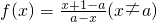
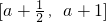 时,求f(x)的值域;
时,求f(x)的值域;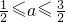 ,求g(x)的最小值.
,求g(x)的最小值.查看答案和解析>>
科目:高中数学 来源:2011届江西省南昌市高三第一次模拟考试数学理卷 题型:解答题
(本小题满分13分)
已知函数
(1)如果对任意 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(2)设实数 的两个极
的两个极 值点分别为
值点分别为 判断①
判断① ②
② ③
③ 是否为定值?若是定值请求出;若不是定值,请把不是定
是否为定值?若是定值请求出;若不是定值,请把不是定 值的表示为函数
值的表示为函数 并求出
并求出 的最小值;
的最小值;
(3)对于(2)中的 设
设 ,试比较
,试比较 (e为自然对数的底)的大小,并证明。
(e为自然对数的底)的大小,并证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com