
(1)求数列{cn}的通项公式;
(2)若数列{cn}的前n项的和为Sn,求![]() ;
;
(3)若不等式![]() +loga(2x+1)(a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.
+loga(2x+1)(a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.
解:(1)∵双曲线方程为![]() =1,焦点为(0,
=1,焦点为(0,![]() ),
),
∴cn=an+an-1.
又∵一条渐近线方程为y=![]() x,
x,
∴ .
.
∴![]() =2.
=2.
∵a1=4,∴{an}是以4为首项的等比数列,
an=2n+1.∴cn=3·2n.
(2)Sn=c1+c2+…+cn=3(2+22+…+2n)=6(2n-1).
∵ancn=3·22n+1,
∴Pn=3(23+25+…+22n+1)=8(22n-1).∴![]() .
.
(3)S=![]() ,①
,①
![]() S=
S=![]() ,②
,②
①-②得S=![]() ,
,
故原不等式等价于![]() +loga(2x+1)(n∈N*)恒成立,
+loga(2x+1)(n∈N*)恒成立,
∴loga(2x+1)≥0恒成立,
故(ⅰ)当a>1时,2x+1≥1,∴x≥0.
(ⅱ)当0<a<1时,0<2x+1≤1-![]() <x≤0.
<x≤0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 2 |
A、an=2
| ||
| B、an=21-n | ||
| C、an=4n-2 | ||
| D、an=2n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| cn |
| 2 |
| 1 |
| c1 |
| 2 |
| c2 |
| n |
| cn |
| n |
| 3•2n |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| cn |
| 2 |
| lim |
| n→∞ |
| ||
| Tn |
| 1 |
| c1 |
| 2 |
| c2 |
| n |
| cn |
| n |
| 3•2n |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省哈尔滨六中高考数学二模试卷(理科)(解析版) 题型:选择题
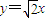 ,其中{an}是以4为首项的正数数列,则数列{an}的通项公式是( )
,其中{an}是以4为首项的正数数列,则数列{an}的通项公式是( )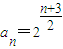
查看答案和解析>>
科目:高中数学 来源:2007-2008学年重庆市南开中学高三(下)3月月考数学试卷(理科)(解析版) 题型:解答题
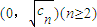 ,且c1=6,一条渐近线方程为
,且c1=6,一条渐近线方程为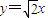 ,其中{an}是以4为首项的正数数列,记Tn=a1c1+a2c2+…+ancn(n∈N*).
,其中{an}是以4为首项的正数数列,记Tn=a1c1+a2c2+…+ancn(n∈N*). ;
;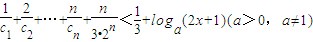 对一切自然数n(n∈N*)恒成立,求实数x的取值范围.
对一切自然数n(n∈N*)恒成立,求实数x的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com