
 ,求随机变量
,求随机变量 的概率分布.
的概率分布. 的概率分布为
的概率分布为 | 0 | 1 | 2 | 3 |
| P | 0.008 | 0.116 | 0.444 | 0.432 |
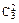 ×0.62×0.4=0.432.
×0.62×0.4=0.432.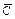 +A
+A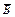 C+
C+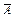 BC)
BC) 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.  的
的 =0)=0.4×0.2×0.1=0.008;
=0)=0.4×0.2×0.1=0.008; =1)=0.6×0.2×0.1+0.4×0.8×0.1+0.4×0.2×0.9=0.116;
=1)=0.6×0.2×0.1+0.4×0.8×0.1+0.4×0.2×0.9=0.116; =2)=0.444;
=2)=0.444; =3)=0.6×0.8×0.9=0.432.
=3)=0.6×0.8×0.9=0.432. 的概率分布为
的概率分布为 | 0 | 1 | 2 | 3 |
| P | 0.008 | 0.116 | 0.444 | 0.432 |


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源:不详 题型:解答题
 ,求
,求 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题






 秒且小于
秒且小于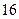 秒认为良好,求该班在这次百米测试中成绩良好的人数;
秒认为良好,求该班在这次百米测试中成绩良好的人数; 的概率。
的概率。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .有放回地摸球,每次摸出一个,有3次摸到红球即停止.
.有放回地摸球,每次摸出一个,有3次摸到红球即停止.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com