
 服从标准正态分布
服从标准正态分布 ,已知
,已知 ,则
,则 ( )
( ) B
B  C
C  D
D 



科目:高中数学 来源:不详 题型:解答题
 两个项目,投资
两个项目,投资 项目
项目 万元,一年后获得的利润为随机变量
万元,一年后获得的利润为随机变量 (万元),根据市场分析,
(万元),根据市场分析, 的分布列为:
的分布列为:| X1 | 12 | 11.8 | 11.7 |
| P |  |  |  |
 项目
项目 万元,一年后获得的利润
万元,一年后获得的利润 (万元)与
(万元)与 项目产品价格的调整(价格上调或下调)有关, 已知
项目产品价格的调整(价格上调或下调)有关, 已知 项目产品价格在一年内进行
项目产品价格在一年内进行 次独立的调整,且在每次调整中价格下调的概率都是
次独立的调整,且在每次调整中价格下调的概率都是 .
. 项目产品价格的下调与一年后获得相应利润的关系如下表:
项目产品价格的下调与一年后获得相应利润的关系如下表: 项目产品价格一年内下调次数 项目产品价格一年内下调次数 (次) (次) |  |  |  |
投资 万元一年后获得的利润 万元一年后获得的利润 (万元) (万元) |  |  |  |
 的方差
的方差 ;
; 的分布列;
的分布列; ,根据投资获得利润的差异,你愿意选择投资哪个项目?
,根据投资获得利润的差异,你愿意选择投资哪个项目? ).
).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 元.
元.| 等级 | 一等品 | 二等品 | 三等品 | 次品 |
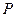 |  |  |  |  |
| 等级 | 一等品 | 二等品 | 三等品 | 次品 |
| 利润 |  |  |  |  |
 的值;
的值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个形状大小完全相同的小球,球的编号分别为
个形状大小完全相同的小球,球的编号分别为 .
. 个球,有放回的抽取3次,求恰有
个球,有放回的抽取3次,求恰有 次抽到
次抽到 号球的概率;
号球的概率; 个球,记球的最大编号为
个球,记球的最大编号为 ,求随机变量
,求随机变量 的分布列.
的分布列.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求
,求 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求随机变量
,求随机变量 的概率分布.
的概率分布.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com