Question

【题目】如图，三棱锥P﹣ABC中，PA=PC，底面ABC为正三角形．
（Ⅰ）证明：AC⊥PB；
（Ⅱ）若平面PAC⊥平面ABC，AC=PC=2，求二面角A﹣PC﹣B的余弦值．

Answer 1

【答案】（Ⅰ）证明：如图，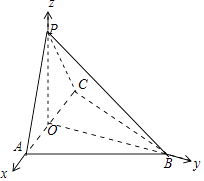

取AC中点O，连接PO，BO，
∵PA=PC，∴PO⊥AC，
又∵底面ABC为正三角形，∴BO⊥AC，
∵PO∩OB=O，∴AC⊥平面POB，则AC⊥PB；
（Ⅱ）解：∵平面PAC⊥平面ABC，且平面PAC∩平面ABC=AC，
PO⊥AC，∴PO⊥平面ABC，
以O为原点，分别以OA、OB、OP所在直线为x、y、z轴建立空间直角坐标系，
∵AC=PC=2，∴P（0，0， ），B（0， ，0），C（﹣1，0，0）， ，
，
设平面PBC的一个法向量为 ，
由 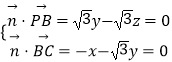，取y=﹣1，得 ，
又 是平面PAC的一个法向量，
∴cos＜ ＞= ．
∴二面角A﹣PC﹣B的余弦值为 ．
【解析】（Ⅰ）取AC中点O，连接PO，BO，由等腰三角形的性质可得PO⊥AC，BO⊥AC，再由线面垂直的判定可得AC⊥平面POB，则AC⊥PB；（Ⅱ）由平面PAC⊥平面ABC，且平面PAC∩平面ABC=AC，可得PO⊥平面ABC，以O为原点，分别以OA、OB、OP所在直线为x、y、z轴建立空间直角坐标系，然后分别求出平面PBC与平面PAC的一个法向量，利用两法向量所成角的余弦值求得二面角A﹣PC﹣B的余弦值．