
【题目】已知函数f(x)=|2x﹣1|+|2x﹣3|,x∈R.
(1)解不等式f(x)≤5;
(2)若不等式m2﹣m<f(x),x∈R都成立,求实数m的取值范围.
【答案】
(1)解:原不等式等价于 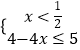 ①,或
①,或 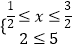 ②,或
②,或 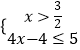 ③.
③.
解①求得 ![]() ,解②求得
,解②求得 ![]() ,解③求得
,解③求得 ![]() ,
,
因此不等式的解集为 ![]()
(2)解:∵f(x)=|2x﹣1|+|2x﹣3|≥|2x﹣1﹣(2x﹣3)|=2,
∴m2﹣m<2,解得﹣1<m<2,
即实数m的取值范围为(﹣1,2).
【解析】(1)原不等式等价于 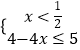 ①,或
①,或 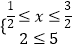 ②,或
②,或 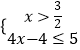 ③.分别求得①、②、③的解集,再取并集,即得所求.(2)利用绝对值三角不等式求得f(x)的最小值为2,可得 m2﹣m<2,由此解得实数m的取值范围.
③.分别求得①、②、③的解集,再取并集,即得所求.(2)利用绝对值三角不等式求得f(x)的最小值为2,可得 m2﹣m<2,由此解得实数m的取值范围.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PA=PC,底面ABC为正三角形.
(Ⅰ)证明:AC⊥PB;
(Ⅱ)若平面PAC⊥平面ABC,AC=PC=2,求二面角A﹣PC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在一个边长为1的正方形AOBC内,曲线y=x3(x>0)和曲线y= ![]() 围成一个叶形图(阴影部分),向正方形AOBC内随机投一点(该点落在正方形AOBC内任何一点是等可能的),则所投的点落在叶形图内部的概率是( )
围成一个叶形图(阴影部分),向正方形AOBC内随机投一点(该点落在正方形AOBC内任何一点是等可能的),则所投的点落在叶形图内部的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lg(x+m)(m∈R);
(1)当m=2时,解不等式 ![]() ;
;
(2)若f(0)=1,且 ![]() 在闭区间[2,3]上有实数解,求实数λ的范围;
在闭区间[2,3]上有实数解,求实数λ的范围;
(3)如果函数f(x)的图像过点(98,2),且不等式f[cos(2nx)]<lg2对任意n∈N均成立,求实数x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知O为坐标原点,双曲线 ![]() (a>0,b>0)的两条渐近线分别为l1 , l2 , 右焦点为F,以OF为直径作圆交l1于异于原点O的点A,若点B在l2上,且
(a>0,b>0)的两条渐近线分别为l1 , l2 , 右焦点为F,以OF为直径作圆交l1于异于原点O的点A,若点B在l2上,且 ![]() =2
=2 ![]() ,则双曲线的离心率等于( )
,则双曲线的离心率等于( )
A.![]()
B.![]()
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0),圆Q:(x﹣2)2+(y﹣
=1(a>b>0),圆Q:(x﹣2)2+(y﹣ ![]() )2=2的圆心Q在椭圆C上,点P(0,
)2=2的圆心Q在椭圆C上,点P(0, ![]() )到椭圆C的右焦点的距离为
)到椭圆C的右焦点的距离为 ![]() .
. 
(1)求椭圆C的方程;
(2)过点P作互相垂直的两条直线l1 , l2 , 且l1交椭圆C于A,B两点,直线l2交圆Q于C,D两点,且M为CD的中点,求△MAB的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),其中0<α<β<π.
=(cosβ,sinβ),其中0<α<β<π.
(1)求证: ![]() 与
与 ![]() 互相垂直;
互相垂直;
(2)若k ![]() 与
与 ![]() ﹣k
﹣k ![]() 的长度相等,求β﹣α的值(k为非零的常数).
的长度相等,求β﹣α的值(k为非零的常数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com