
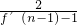 ,求证:(
,求证:(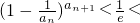
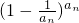 ;
;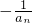 ,Tn为数列{bn}的前n项和,求证:T2011-1<ln2011<T2010.
,Tn为数列{bn}的前n项和,求证:T2011-1<ln2011<T2010.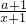 =
=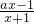 ,
, (a>0),
(a>0), )时,f′(x)<0,函数f(x)在(-1,
)时,f′(x)<0,函数f(x)在(-1, )内单调递增;
)内单调递增; ,+∞)时,f′(x)>0,函数f(x)在(
,+∞)时,f′(x)>0,函数f(x)在( ,+∞)内单调递减,
,+∞)内单调递减, ),增区间是(
),增区间是( ,+∞);
,+∞); ,
,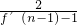 =-n,
=-n,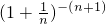 <
< <
<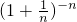 ?
?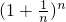 <e<
<e<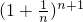 ?nln(1+
?nln(1+ )<1<(n+1)ln(1+
)<1<(n+1)ln(1+ )
) <ln
<ln <
< ,
, =
= ,
, )>g(0)=0?
)>g(0)=0? -ln(1+
-ln(1+ )>0,①
)>0,① ,x∈[0,+∞),
,x∈[0,+∞), -
-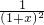 =
= ,
, )>φ(0)=0,
)>φ(0)=0, )-
)-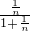 >0?
>0? <ln(1+n)②,
<ln(1+n)②, <ln
<ln <
< ,即
,即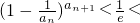
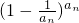 ;
; =
= ,则Tn=1+
,则Tn=1+ +
+ +…+
+…+ ,
, <ln
<ln <
< ,
, +
+ +…+
+…+ <ln
<ln +ln
+ln +…+ln
+…+ln <1+
<1+ +
+ +…+
+…+ ,
, <ln
<ln <
< ,令g(x)=x-ln(1+x),求出g(x)的导函数,找出g(x)的单调增区间为(0,+∞),又根据g(x)在x=0处连续,所以得到g(
,令g(x)=x-ln(1+x),求出g(x)的导函数,找出g(x)的单调增区间为(0,+∞),又根据g(x)在x=0处连续,所以得到g( )大于g(0),化简后得到一个不等式,记作①,然后令φ(x)=ln(x+1)-
)大于g(0),化简后得到一个不等式,记作①,然后令φ(x)=ln(x+1)- ,求出φ(x)的导函数,根据导函数大于0,找出φ(x)的增区间为[0,+∞),也得到φ(
,求出φ(x)的导函数,根据导函数大于0,找出φ(x)的增区间为[0,+∞),也得到φ( )大于φ(0),代入化简后得到令一个不等式,记作②,联立①②,得证;
)大于φ(0),代入化简后得到令一个不等式,记作②,联立①②,得证;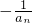 ,得到bn的通项,罗列出前n项的和Tn的各项,再根据(Ⅱ)的结论,分别令n=1,2,…,2010,代入不等式中,将各式相加,利用对数的运算法则及已知化简后,得证.
,得到bn的通项,罗列出前n项的和Tn的各项,再根据(Ⅱ)的结论,分别令n=1,2,…,2010,代入不等式中,将各式相加,利用对数的运算法则及已知化简后,得证.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
| 2 | 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 | 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2•2x | 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2•2x | 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com