
已知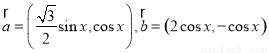 ,函数
,函数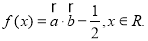
(1)求函数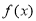 的最小值和最小正周期;
的最小值和最小正周期;
(2)设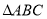 的内角
的内角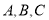 的对边分别为
的对边分别为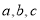 ,且
,且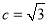 ,
,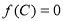 ,若
,若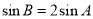 ,求
,求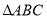 的面积.
的面积.
(1)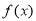 的最小值为
的最小值为 ,最小正周期为
,最小正周期为 (2)
(2)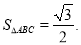
【解析】
试题分析:(1)利用两角和正弦公式和降幂公式化简,得到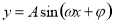 的形式,利用公式
的形式,利用公式
 计算周期.(2)求三角函数的最小正周期一般化成
计算周期.(2)求三角函数的最小正周期一般化成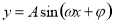 ,
, ,
,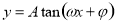 形式,利用周期公式即可.(3)求解较复杂三角函数的最值时,首先化成
形式,利用周期公式即可.(3)求解较复杂三角函数的最值时,首先化成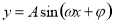 形式,在求最大值或最小值;(4)1)在解决三角形的问题中,面积公式
形式,在求最大值或最小值;(4)1)在解决三角形的问题中,面积公式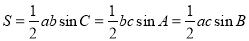 最常用,因为公式中既有边又有角,容易和正弦定理、余弦定理联系起来.
最常用,因为公式中既有边又有角,容易和正弦定理、余弦定理联系起来.
试题解析:【解析】
(1) ,
,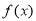 的最小值为
的最小值为 ,最小正周期为
,最小正周期为 3分
3分
(2)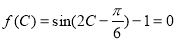 ,则
,则 .
.
∵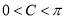 ,∴
,∴ ,因此
,因此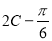 =
=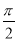 ,∴
,∴ . 5分
. 5分
∵ 及正弦定理,得
及正弦定理,得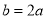 .①
.①
由余弦定理,得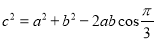 ,且
,且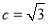 ,
,
∴ . ②
. ②
由①②联立,得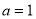 ,
, . 7分
. 7分
 8分
8分
考点:(1)三角函数的化简和求值;(2)求三角形的面积.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源:2016届甘肃省嘉峪关市高一下学期期末联考数学试卷(解析版) 题型:选择题
已知f(x)=2sin(ωx+φ)的部分图象如图所示,则f(x)的表达式为( ).
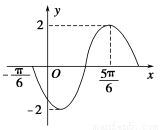
A.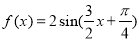 B.
B.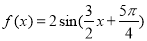
C.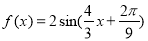 D.
D.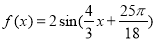
查看答案和解析>>
科目:高中数学 来源:2016届甘肃省高一下学期期中考试数学试卷(解析版) 题型:选择题
若P(A+B)=P(A)+P(B)=1,则事件A与B的关系是( )
A.互斥不对立 B.对立不互斥 C.互斥且对立 D.以上答案都不对
查看答案和解析>>
科目:高中数学 来源:2016届甘肃兰州一中高一下学期期末考试数学试卷(解析版) 题型:选择题
给出下列命题
① 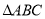 中,
中, ,
, ,则
,则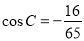 ;
;
② 角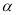 终边上一点
终边上一点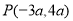 ,且
,且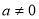 ,那么
,那么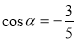 ;
;
③ 若函数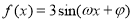 对于任意的
对于任意的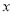 都有
都有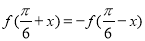 ,则
,则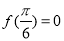 ;
;
④ 已知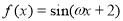 满足
满足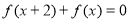 ,则
,则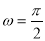 .
.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2016届湖南省高一下学期6月五科联赛数学试卷(解析版) 题型:选择题
设等差数列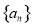 满足
满足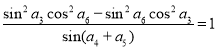 ,公差
,公差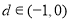 ,当且仅当
,当且仅当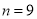 时,数列
时,数列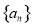 的前
的前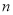 项和
项和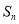 取得最大值,求该数列首项
取得最大值,求该数列首项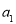 的取值范围
的取值范围
A.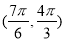 B.
B.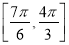 C.
C.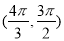 D.
D.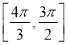
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com