
(2014•包头二模)过双曲线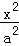 ﹣
﹣ =1(a>0,b>0)的左焦点F1(﹣c,0)(c>0)作圆x2+y2=
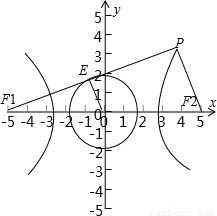
=1(a>0,b>0)的左焦点F1(﹣c,0)(c>0)作圆x2+y2= 的切线,切点为E,直线F1E交双曲线右支于点P,若
的切线,切点为E,直线F1E交双曲线右支于点P,若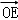 =
= (
(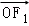 +
+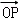 ),则双曲线的离心率为( )
),则双曲线的离心率为( )
A.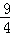 B.
B. C.
C. D.
D.
C
【解析】
试题分析:先确定E为F1P的中点,所以OE为△PF1F2的中位线,进而得到|PF2|=a,|F1F2|=2c,|PF1|=2a+a=3a,PF1切圆O于E,可得PF2⊥PF1,由勾股定理得出关于a,c的关系式,最后即可求得离心率.
【解析】
∵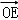 =
=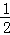 (
( +
+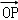 ),∴E为F1P的中点,
),∴E为F1P的中点,
∵O为F1F2的中点,
∴OE为△PF1F2的中位线,
∴OE∥PF2,|OE|=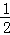 |PF2|,
|PF2|,
∵|OE|=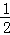 a
a
∴|PF2|=a
∵PF1切圆O于E
∴OE⊥PF1
∴PF2⊥PF1,
∵|F1F2|=2c,|PF1|﹣|PF2|=2a⇒|PF1|=2a+a=3a,
∴由勾股定理a2+9a2=4c2
∴10a2=4c2,
∴e=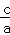 =
=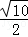 .
.
故选:C.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2014•防城港一模)空间四边形ABCD中,AB=BC=CD=DA=BD=AC,E是AB的中点,若CE与平面BCD所成的角为θ,则( )
A.sinθ=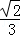 B.sinθ=
B.sinθ=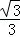 C.cosθ=
C.cosθ=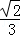 D.cosθ=
D.cosθ=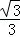
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.2空间中向量的概念和运算练习卷(解析版) 题型:?????
已知ABCD为矩形,P为平面ABCD外一点,且PA⊥平面ABCD,G为△PCD的重心,若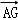 =x
=x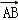 +y
+y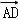 +z
+z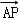 ,则( )
,则( )
A.x= ,y=
,y= ,z=
,z=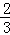
B.x= ,y=
,y=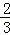 ,z=
,z=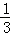
C.x=﹣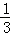 ,y=
,y=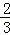 ,z=
,z=
D.x=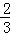 ,y=
,y= ,z=
,z=
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.1尝试用向量处理空间图形练习卷(解析版) 题型:?????
若{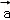 、
、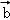 、
、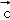 }为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
}为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
A.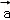 ,
,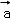 +
+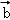 ,
,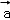 ﹣
﹣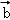
B.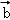 ,
,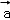 +
+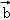 ,
,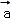 ﹣
﹣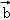
C.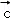 ,
,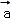 +
+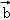 ,
,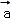 ﹣
﹣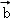
D.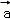 +
+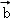 ,
,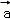 ﹣
﹣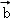 ,
,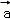 +2
+2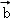
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.1尝试用向量处理空间图形练习卷(解析版) 题型:?????
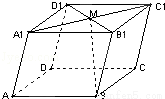
如图:在平行六面体ABCD﹣A1B1C1D1中,M为A1C1与B1D1的交点.若 ,
, ,
, ,则下列向量中与
,则下列向量中与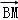 相等的向量是( )
相等的向量是( )
A.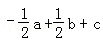 B.
B.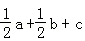 C.
C.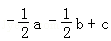 D.
D.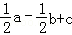
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 2.4圆锥曲线的应用练习卷(解析版) 题型:?????
(2014•南宁一模)直线l:x=a与圆x2+y2=4和抛物线y2=3 x分别相交于A、B和C、D点,若|CD|=3|AB|,则a的值为( )
x分别相交于A、B和C、D点,若|CD|=3|AB|,则a的值为( )
A.﹣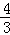
 B.
B. C.
C.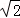 D.
D.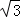 或﹣
或﹣
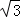
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 2.4圆锥曲线的应用练习卷(解析版) 题型:?????
(2014•红桥区一模)若双曲线mx2+ny2=1的一个焦点与抛物线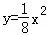 的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )
的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )
A.y2+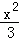 =1 B.y2﹣
=1 B.y2﹣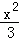 =1 C.
=1 C.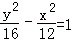 D.
D.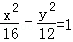
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 7.4副数的几何表示练习卷(解析版) 题型:?????
(2014•重庆)实部为﹣2,虚部为1的复数所对应的点位于复平面内的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 7.2复数的概念练习卷(解析版) 题型:?????
(2015•重庆一模)复数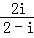 所对应的点位于复平面内( )
所对应的点位于复平面内( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com