
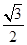 ,c=2,A=60º,求a,b的值;
,c=2,A=60º,求a,b的值;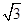 ,b=1,(2)直角三角形或等腰三角形
,b=1,(2)直角三角形或等腰三角形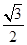 =
=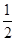 bcsinA=bsin60º,∴b=1.再由余弦定理a2=b2+c2-2bccosA=3,∴a=
bcsinA=bsin60º,∴b=1.再由余弦定理a2=b2+c2-2bccosA=3,∴a=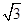 .(2)由正弦定理得2RsinA=a,2RsinB=b,∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,由已知A、B为三角形内角,∴A+B=90º或A=B.∴△ABC为直角三角形或等腰三角形.本题也可从余弦定理出发:
.(2)由正弦定理得2RsinA=a,2RsinB=b,∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,由已知A、B为三角形内角,∴A+B=90º或A=B.∴△ABC为直角三角形或等腰三角形.本题也可从余弦定理出发: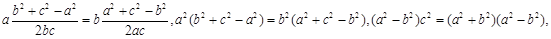 所以
所以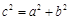 或
或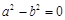 .
.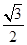 =
=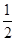 bcsinA=bsin60º,∴b=1.
bcsinA=bsin60º,∴b=1.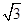 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:单选题
 间的距离,李宁同学首先选定了与
间的距离,李宁同学首先选定了与 不共线的一点
不共线的一点 ,然后给出了三种测量方案:(
,然后给出了三种测量方案:( 的角
的角 所对的边分别记为
所对的边分别记为 ):
): ② 测量
② 测量 ③测量
③测量
 间距离的所有方案的序号为( )
间距离的所有方案的序号为( )
| A.①② | B.②③ | C.①③ | D.①②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
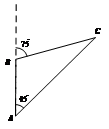
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com