数学归纳法适用于证明的命题类型是
A．已知 结论 | B．结论已知 | C．直接证明比较困难 | D．与正整数有关 |
阅读快车系列答案科目：高中数学 来源： 题型：单选题
在平面上，我们如果用一条直线去截正方形的一个角，那么截下的一个直角三角形，按图所标边长，由勾股定理有：c2＝a2＋b2。设想正方形换成正方体，把截线换成如下图的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥O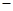
LMN，如果用S1，S2，S3表示三个侧面面积，S4表示截面面积，那么你类比得到的结论是 ．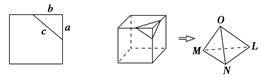 
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
观察式子：1＋
<
，1＋＋
<
，1＋＋＋
<
， ，则可归纳出一般式子为( )
A．1＋＋＋ ＋ < (n≥2) | B．1＋＋＋ ＋< (n≥2) |
C．1＋＋＋ ＋< (n≥2) | D．1＋＋＋ ＋< (n≥2) |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
在平面上，我们如果用一条直线去截正方形的一个角，那么截下的一个直角三角形，按图所标边长，由勾股定理有：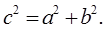
设想正方形换成正方体，把截线换成如图的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN，如果用
表示三个侧面面积，
表示截面面积，那么你类比得到的结论是（ ）
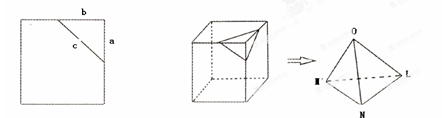
A． | B． |
C． | D． |
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
设ΔABC的三边长分别为
、
、
，ΔABC的面积为
，则ΔABC的内切圆半径为
，
将此结论类比到空间四面体：设四面体S—ABCD的四个面的面积分别为
，
，
，
，
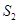体积为
，则四面体的内切球半径
= ．
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
用反证法证明“a，b，c中至少有一个大于0”，下列假设正确的是（ ）
| A．假设a，b，c都小于0 |
| B．假设a，b，c都大于0 |
| C．假设a，b，c中都不大于0 |
| D．假设a，b，c中至多有一个大于0 |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
下列表述正确的是 ( )
①归纳推理是由部分到整体的推理；②归纳推理是由一般到一般的推理；③演绎推理是由一般到特殊的推理；④类比推理是由特殊到一般的推理；⑤类比推理是由特殊到特殊的推理．
| A．①②③ | B．②③④ |
| C．②④⑤ | D．①③⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
…，依它的10项的规律，则a99+a100的值为（ ）
