
����Ŀ��һ����ѧ�����Կ���С�����ꡱ����һ��ѧϰ��Ʒ��������ÿ�۳�1�иDz�Ʒ����30Ԫ��δ�۳�����Ʒÿ�п���10Ԫ������ͳ�����ϣ��õ�����Ʒ������������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ������ͬѧΪ�˹���180�иò�Ʒ����x����λ���У�100��x��200����ʾһ�����ڵ��г���������y����λ��Ԫ����ʾһ�����ھ����ò�Ʒ������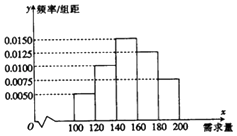
��1������ֱ��ͼ������������г�������x��ƽ������
��2����y��ʾΪx�ĺ�����
��3������ֱ��ͼ�����������������3800Ԫ�ĸ��ʣ���Ƶ�ʽ��Ƹ��ʣ���
���𰸡�
��1���⣺��Ƶ�ʷֲ�ֱ��ͼ�ã�
��������[100��120���ڵ�Ƶ��Ϊ��0.005��20=0.1��
��������[120��140���ڵ�Ƶ��Ϊ��0.01��20=0.2��
��������[140��160���ڵ�Ƶ��Ϊ��0.015��20=0.3��
��������[160��180���ڵ�Ƶ��Ϊ��0.0125��20=0.25��
��������[180��200]�ڵ�Ƶ��Ϊ��0.0075��20=0.15��
�����ֱ��ͼ������������г�������x��ƽ������
![]() =110��0.1+130��0.2+150��0.3+170��0.25+190��0.15=153��
=110��0.1+130��0.2+150��0.3+170��0.25+190��0.15=153��
��2���⣺��ÿ�۳�1�иDz�Ʒ����30Ԫ��δ�۳�����Ʒÿ�п���10Ԫ��
�൱100��x��180ʱ��y=30x��10��180��x��=40x��1800��
��180��x��200ʱ��y=30��180=5400��
��y= ![]()
��3���⣺����������3800Ԫ��
��40x��1800��3800����x��140��
���ɣ�1��֪��������3800Ԫ�ĸ���Ϊ��
1��0.1��0.2=0.7��
��������1����Ƶ�ʷֲ�ֱ��ͼ����������ָ����Χ�ڵ�Ƶ��ֵ�ٸ���ֱ��ͼ������������г�������x��ƽ������
2����������ɵú�������ʽ��100��x��180��һ�κ�������180<x��2 00�dz�������
3��������ɵ���������3800Ԫ���õ�x��140���������֪֪��������3800Ԫ�ĸ���Ϊ��1��0.1��0.2=0.7��
�����㾫��������Ƶ�ʷֲ�ֱ��ͼ�ǽ����ĸ�������Ҫ֪��Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC���ܳ�Ϊ ![]() +1����sinA+sinB=
+1����sinA+sinB= ![]() sinC
sinC
��I�����AB�ij���
��������ABC�����Ϊ ![]() sinC�����C�Ķ�����
sinC�����C�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������p��ʵ������x2��4ax+3a2��0��a��0������q��ʵ������ ![]() ��0��
��0��
��1����a=1��p��qΪ�����⣬��x��ȡֵ��Χ��
��2�����Vp�ǩVq�ij�ֲ���Ҫ��������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij����������P��Q�����ͺŵIJ����ֱַ������ȡ8����Ʒ���м�飬����Ӳ��ϵ������ͳ�ƣ�ͳ�������þ�Ҷͼ��ʾ����ͼ��ʾ������P�����ݵ�������Q�����ݵ���λ���ֱ�Ϊ�� ��
A.22��22.5
B.21.5��23
C.22��22
D.21.5��22.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=ln��x+1��+a��x2��x����a��0��
��1����a=1ʱ������f��x���ļ�ֵ��
��2����x��0��f��x����0��������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ���4x��m2x+1+4=0��ʵ��������m��ȡֵ��Χ�� ��
A.��1��+�ޣ�
B.[1��+�ޣ�
C.��2��+�ޣ�
D.[2��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=a2x��2��x������ΪR���溯����
��1����ʵ��a��ֵ��
��2���жϺ���f��x����R�ϵĵ����ԣ������ú��������ԵĶ���֤����
��3��������ʽf��9x+1��+f��t��23x+5����0����R�Ϻ��������ʵ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x���Ƕ�����[��1��1]�ϵ��溯������f��1��=1����a��b��[��1��1]��a+b��0ʱ���� ![]() ��0������
��0������
�����ж�f��x����[��1��1]�ϵĵ����ԣ���֤����
���ⲻ��ʽ��f��2x��1����f��1��3x����
������f��x����m2��2am+1�����е�a��[��1��1]���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=Asin����x+�գ���A��0���أ�0��|��|�� ![]() ����ͼ����ͼ��ʾ��
����ͼ����ͼ��ʾ��
��1����ȷ���ú����Ľ���ʽ��
��2���ú�����ͼ�ǿ���y=sinx��x��R����ͼ��������ƽ�ƺ������任�õ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com