
【题目】已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的图象如图所示.
)的图象如图所示.
(1)试确定该函数的解析式;
(2)该函数的图角可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
【答案】
(1)解:∵由图知:A=2,
∴T=2( ![]() ﹣
﹣ ![]() )=π,
)=π,
∴T= ![]() ,可得:ω=2,
,可得:ω=2,
∴y=2sin(2x+φ),
把( ![]() ,2)代入得2sin(
,2)代入得2sin( ![]() +φ)=2,
+φ)=2,
可得:sin( ![]() +φ)=1,
+φ)=1,
∵|φ|< ![]() ,
,
∴ ![]() +φ=
+φ= ![]() ,可得:φ=﹣
,可得:φ=﹣ ![]() ,
,
∴y=2sin(2x﹣ ![]() )
)
(2)解:y=2sin(2x﹣ ![]() )的图象可由y=sinx的图象
)的图象可由y=sinx的图象
先向右平移 ![]() 个单位长度,再保持纵坐标不变横坐标缩短为原来的
个单位长度,再保持纵坐标不变横坐标缩短为原来的 ![]() 倍,最后保持横坐标不变纵坐标伸长为原来的2倍得到.
倍,最后保持横坐标不变纵坐标伸长为原来的2倍得到.
(或先保持纵坐标不变横坐标缩短为原来的 ![]() 倍,再向右平移
倍,再向右平移 ![]() 个单位长度,最后保持横坐标不变纵坐标伸长为原来的2倍得到.)
个单位长度,最后保持横坐标不变纵坐标伸长为原来的2倍得到.)
【解析】1、根据图像可得,A=2,![]() =π,求得ω=2,把(
=π,求得ω=2,把( ![]() ,2)代入即可求得φ的值,即得函数的解析式。
,2)代入即可求得φ的值,即得函数的解析式。
2、根据函数y=Asin(ωx+φ)的图象变换可得。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一名大学生尝试开家小“网店”销售一种学习用品,经测算每售出1盒盖产品获利30元,未售出的商品每盒亏损10元.根据统计资料,得到该商品的月需求量的频率分布直方图(如图所示),该同学为此购进180盒该产品,以x(单位:盒,100≤x≤200)表示一个月内的市场需求量,y(单位:元)表示一个月内经销该产品的利润.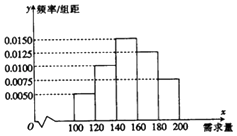
(1)根据直方图估计这个月内市场需求量x的平均数;
(2)将y表示为x的函数;
(3)根据直方图估计这个月利润不少于3800元的概率(用频率近似概率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2 ![]() ,
, ![]() ).
).
(Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为(﹣1,1),满足f(﹣x)=﹣f(x),且f(
的定义域为(﹣1,1),满足f(﹣x)=﹣f(x),且f( ![]() )=
)= ![]() .
.
(1)求函数f(x)的解析式;
(2)证明f(x)在(﹣1,1)上是增函数;
(3)解不等式f(x2﹣1)+f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() [cos(2x+
[cos(2x+ ![]() )+4sinxcosx]+1,x∈R.
)+4sinxcosx]+1,x∈R.
(1)求函数f(x)的最小正周期;
(2)令g(x)=af(x)+b,若函数g(x)在区间[﹣ ![]() ,
, ![]() ]上的值域为[﹣1.1],求a+b的值.
]上的值域为[﹣1.1],求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx,x∈(0,2π),点P(x,y)是函数f(x)图象上任一点,其中0(0,0),A(2π,0),记△OAP的面积为g(x),则g′(x)的图象可能是( )
A.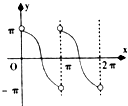
B.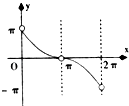
C.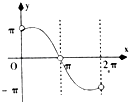
D.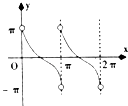
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x+2y-2=0,试求:
(1)点P(-2,-1)关于直线l的对称点坐标;
(2)直线 ![]() 关于直线l对称的直线l2的方程;
关于直线l对称的直线l2的方程;
(3)直线l关于点(1,1)对称的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com