
【题目】如图,在三棱锥P﹣ABC中,AB=AC=2PA=2,∠PAB=∠PAC=∠BAC= ![]() .
.
(Ⅰ) 证明:AP⊥BC;
(Ⅱ)求三棱锥P﹣ABC的体积.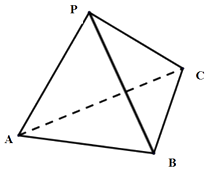
【答案】(Ⅰ)证明:由已知可得 ![]() ,
,
由余弦定理得 ![]() ,则AB2=PB2+AP2 ,
,则AB2=PB2+AP2 ,
∴AP⊥PB,同理AP⊥PC,又PB∩PC=P.
∴AP⊥平面PBC,则AP⊥BC;
(Ⅱ) 解:在Rt△APB中,由AB=2PA=2,得PB= ![]() ,
,
同理求得PC= ![]() ,又∠BAC=
,又∠BAC= ![]() ,∴BC=2,
,∴BC=2,
∴△PBC边BC上的高为 ![]() ,
,
则 ![]() .
.
∵VP﹣ABC=VA﹣PBC ,
∴ ![]()
【解析】(Ⅰ)由已知结合余弦定理求得PB、PC的长度,可得AP⊥PB,AP⊥PC,再由线面垂直的判定可得AP⊥平面PBC,则AP⊥BC;(Ⅱ)求解直角三角形可得PB=PC= ![]() ,又∠BAC=
,又∠BAC= ![]() ,得BC=2,进一步求出△PBC边BC上的高,得到
,得BC=2,进一步求出△PBC边BC上的高,得到 ![]() .结合VP﹣ABC=VA﹣PBC可得
.结合VP﹣ABC=VA﹣PBC可得
三棱锥P﹣ABC的体积.
【考点精析】利用空间中直线与直线之间的位置关系对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】已知{an}是公差为1的等差数列,a1 , a5 , a25成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=3 ![]() +an , 求数列{bn}的前n项和Tn .
+an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 已知a3=24,S11=0.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn;
(Ⅲ)当n为何值时,Sn最大,并求Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:
五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:
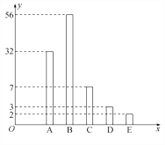
(1)试估算该校高三年级学生获得成绩为![]() 的人数;
的人数;
(2)若等级![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别对应100分、90分、80分、70分、60分,学校要求当学生获得的等级成绩的平均分大于90分时,高三学生的考前心理稳定,整体过关,请问该校高三年级目前学生的考前心理稳定情况是否整体过关?
分别对应100分、90分、80分、70分、60分,学校要求当学生获得的等级成绩的平均分大于90分时,高三学生的考前心理稳定,整体过关,请问该校高三年级目前学生的考前心理稳定情况是否整体过关?
(3)以每个学生的心理都培养成为健康状态为目标,学校决定对成绩等级为![]() 的16名学生(其中男生4人,女生12人)进行特殊的一对一帮扶培训,从按分层抽样抽取的4人中任意抽取2名,求恰好抽到1名男生的概率..
的16名学生(其中男生4人,女生12人)进行特殊的一对一帮扶培训,从按分层抽样抽取的4人中任意抽取2名,求恰好抽到1名男生的概率..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.57.2,3.6
B.57.2,56.4
C.62.8,63.6
D.62.8,3.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com