
分析 (1)利用等差数列的通项公式与求和公式即可得出.
(2)${b_n}={3^n}•{a_n}$=(2n+1)•3n,利用“错位相减”法与等比数列的求和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵a3=7,a5+a7=26,∴a1+2d=7,2a1+10d=26,
联立解得a1=3,d=2.
∴an=3+2(n-1)=2n+1,
Sn=$\frac{n(3+2n+1)}{2}$=n2+2n.
(2)${b_n}={3^n}•{a_n}$=(2n+1)•3n.
∴数列{bn}的前n项和Tn=3×3+5×32+7×33+…+(2n+1)•3n,
3Tn=3×32+5×33+…+(2n-1)•3n+(2n+1)•3n+1,
∴-2Tn=9+2×(32+33+…+3n)-(2n+1)•3n+1=3+2×$\frac{3({3}^{n}-1)}{3-1}$-(2n+1)•3n+1=-2n•3n+1,
∴Tn=n•3n+1.
点评 本题考查了等差数列与等比数列通项公式与求和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
| A. | 非p:?x∈R,x<sin x | B. | 非p:?x∈R,x≤sin x | ||
| C. | 非p:?x∈R,x≤sin x | D. | 非p:?x∈R,x<sin x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 0 | 1 | 4 | 5 | 6 | 8 |
| y | 1.3 | 1.8 | 5.6 | 6.1 | 7.4 | 9.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,△BCD为等边三角形,PA=BD=$\sqrt{3}$,AB=AD,E为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,△BCD为等边三角形,PA=BD=$\sqrt{3}$,AB=AD,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
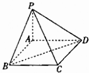 如图,四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD是菱形.
如图,四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD是菱形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com