
【题目】已知数列{an}的前n项和Sn=2n+2-4.
(1)求数列{an}的通项公式;
(2)设bn=an·log2an,求数列{bn}的前n项和Tn.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)由题意,分类讨论n≥2和n=1两种情况可得数列{an}的通项公式为an=2n+1,n∈N*.
(2)结合(1)的结果可知bn=anlog2an=(n+1)·2n+1,错位相减可得数列{bn}的前n项和Tn=n·2n+2.
试题解析:
(1)由题意,Sn=2n+2-4,
n≥2时,an=Sn-Sn-1=2n+2-2n+1=2n+1,
当n=1时,a1=S1=23-4=4,也适合上式,
∴数列{an}的通项公式为an=2n+1,n∈N*.
(2)∵bn=anlog2an=(n+1)·2n+1,
∴Tn=2·22+3·23+4·24+…+n·2n+(n+1)·2n+1,①
2Tn=2·23+3·24+4·25+…+n·2n+1+(n+1)·2n+2.②
②-①得,
Tn=-23-23-24-25-…-2n+1+(n+1)·2n+2
=-23-![]() +(n+1)·2n+2
+(n+1)·2n+2
=-23-23(2n-1-1)+(n+1)·2n+2
=(n+1)·2n+2-23·2n-1
=(n+1)·2n+2-2n+2=n·2n+2.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆心在x轴上,半径为2的圆C位于y轴右侧,且与直线x- y+2=0相切.
(1)求圆C的方程.
(2)在圆C上,是否存在点M(m,n),使得直线l:mx+ny=1与圆O:x2+y2=1相交于不同的两点A,B,且△OAB的面积最大?若存在,求出点M的坐标及对应的△OAB的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂每日生产一种产品![]() 吨,每日生产的产品当日销售完毕,日销售额为
吨,每日生产的产品当日销售完毕,日销售额为![]() 万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了
万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了![]() 的一组统计数据如下表:
的一组统计数据如下表:

(1)请判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() 之间的关系?可从函数增长趋势方面给出简单的理由;
之间的关系?可从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并估计当日产量
的回归方程,并估计当日产量![]() 时,日销售额是多少?(结果保留整数)
时,日销售额是多少?(结果保留整数)
参考公式及数据:线性回归方程![]() 中,
中, ,
,![]() .
.
![]() ,
,![]()
![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() (n∈N*)
(n∈N*)
(1)求![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(3)若![]() 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各射击一次,击中目标的概率分别是 ![]() 和
和 ![]() .假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
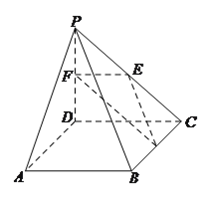
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
(![]() )求四棱锥
)求四棱锥![]() 的体积.
的体积.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )在线段
)在线段![]() 上确定一点
上确定一点![]() ,使
,使![]() 平面
平面![]() ,并给出证明.
,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 某人打靶,射击10次,击中7次,那么此人中靶的概率为0.7
B. 一位同学做掷硬币试验,掷6次,一定有3次“正面朝上”
C. 某地发行福利彩票,回报率为![]() ,有人花了100元钱买彩票,一定会有47元的回报
,有人花了100元钱买彩票,一定会有47元的回报
D. 概率等于1的事件不一定为必然事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com