【题目】为了培养学生的安全意识，某中学举行了一次“安全自救”的知识竞赛活动，共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，得到如下的频率分布表，请你根据频率分布表解答下列问题：
序号（i） | 分组（分数） | 组中值（Gi） | 频数（人数） | 频率（fi） |
1 |
| 65 | ① | 0.10 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.20 |
4 |
| 95 | ④ | ⑤ |
合计 | 50 | 1.00 | ||
（1）求出频率分布表中①②③④⑤处的值；
（2）为鼓励更多的学生了解“安全自救”知识，成绩不低于85分的学生能获奖，请估计在参加的800名学生中大约有多少名学生能获奖；
（3）求这800名学生的平均分.
科目：高中数学 来源： 题型：
【题目】学校书店新进了一套精品古典四大名著：《红楼梦》、《三国演义》、《西游记》、《水浒传》共四本书，每本名著数量足够多，今有五名同学去书店买书，由于价格较高，五名同学打算每人只选择一本购买.
（1）求“每本书都有同学买到”的概率；
（2）求“对于每个同学，均存在另一个同学与其购买的书相同”的概率；
（3）记X为五位同学购买相同书的个数的最大值，求X的分布列和数学期望E（X）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）的图象向左平移1个单位后关于y轴对称，当x2＞x1＞1时，[f（x2）﹣f（x1）]（x2﹣x1）＜0恒成立，设a＝f（
），b＝f（2），c＝f（3），则a、b、c的大小关系为（ ）
A.c＞a＞bB.c＞b＞aC.a＞c＞bD.b＞a＞c
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
为奇函数，
，其中
.
（1）若函数
的图像过点
，求实数
和
的值；
（2）若
，试判断函数
在
上的单调性并证明；
（3）设函数
，若对每一个不小于3的实数
，都恰有一个小于3的实数
，使得
成立，求实数的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线C的参数方程为
（
为参数），以直角坐标系的原点o为极点，x轴的正半轴为极轴，建立极坐标系，直线l的极坐标方程是：
（Ⅰ）求曲线C的普通方程和直线l的直角坐标方程：
（Ⅱ）点P是曲线C上的动点，求点P到直线l距离的最大值与最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从全校参加数学竞赛的学生的试卷中抽取一个样本，考察竞赛的成绩分布，将样本分成5组，绘制成频率分布直方图，图中从左到右各组的小长方形的高之比为1∶3∶6∶4∶2，最右边一组的频数是6，请结合直方图提供的信息，解答下列问题：
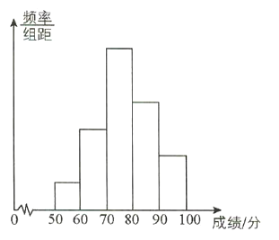
（1）样本的容量是多少？
（2）列出频率分布表.
（3）成绩落在哪一组内的人数最多？并求出该组的频数、频率.
（4）估计这次竞赛中，成绩不低于60分的学生人数占总人数的百分比.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
的图象关于原点对称，其中a为常数.
（1）求a的值，并写出函数f（x）的单调区间（不需要求解过程）；
（2）若关于x的方程
在[2，3]上有解，求k的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设椭圆
的焦点分别为
、
，直线
：
交
轴于点
，且
（1）求椭圆的方程；
（2）过
分别作互相垂直的两直线
，与椭圆分别交于D、E和M、N四点， 求四边形
面积的最大值和最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
