
【题目】设椭圆![]() 的焦点分别为
的焦点分别为![]() 、
、![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]()
(1)求椭圆的方程;
(2)过![]() 分别作互相垂直的两直线
分别作互相垂直的两直线![]() ,与椭圆分别交于D、E和M、N四点, 求四边形
,与椭圆分别交于D、E和M、N四点, 求四边形![]() 面积的最大值和最小值.
面积的最大值和最小值.
科目:高中数学 来源: 题型:
【题目】为了培养学生的安全意识,某中学举行了一次“安全自救”的知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:
序号(i) | 分组(分数) | 组中值(Gi) | 频数(人数) | 频率(fi) |
1 |
| 65 | ① | 0.10 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.20 |
4 |
| 95 | ④ | ⑤ |
合计 | 50 | 1.00 | ||
(1)求出频率分布表中①②③④⑤处的值;
(2)为鼓励更多的学生了解“安全自救”知识,成绩不低于85分的学生能获奖,请估计在参加的800名学生中大约有多少名学生能获奖;
(3)求这800名学生的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点坐标分别是
的两个焦点坐标分别是![]() 、
、![]() ,并且经过点
,并且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() :
:![]() 相切,并与椭圆
相切,并与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() .当
.当![]() ,且满足
,且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若实数![]() 满足
满足![]() ,称
,称![]() 为函数
为函数![]() 的不动点.有下面三个命题:(1)若
的不动点.有下面三个命题:(1)若![]() 是二次函数,且没有不动点,则函数
是二次函数,且没有不动点,则函数![]() 也没有不动点;(2)若
也没有不动点;(2)若![]() 是二次函数,则函数
是二次函数,则函数![]() 可能有
可能有![]() 个不动点;(3)若
个不动点;(3)若![]() 的不动点的个数是
的不动点的个数是![]() ,则
,则![]() 的不动点的个数不可能是
的不动点的个数不可能是![]() ;它们中所有真命题的序号是________________________.
;它们中所有真命题的序号是________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在《爸爸去哪儿》第二季第四期中,村长给6位“萌娃”布置一项搜寻空投食物的任务.已知:①食物投掷地点有远、近两处;②由于Grace年纪尚小,所以要么不参与该项任务,但此时另需一位小孩在大本营陪同,要么参与搜寻近处投掷点的食物;③所有参与搜寻任务的小孩须被均分成两组,一组去远处,一组去近处,那么不同的搜寻方案有______种.(以数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对定义在![]() 上的函数
上的函数![]() 和常数
和常数![]() ,
,![]() ,若
,若![]() 恒成立,则称
恒成立,则称![]() 为函数
为函数![]() 的一个“凯森数对”.
的一个“凯森数对”.
(1)若![]() 是
是![]() 的一个“凯森数对”,且
的一个“凯森数对”,且![]() ,求
,求![]() ;
;
(2)已知函数![]() 与
与![]() 的定义域都为
的定义域都为![]() ,问它们是否存在“凯森数对”?分别给出判断并说明理由;
,问它们是否存在“凯森数对”?分别给出判断并说明理由;
(3)若![]() 是
是![]() 的一个“凯森数对”,且当
的一个“凯森数对”,且当![]() 时,
时,![]() ,求
,求![]() 在区间
在区间![]() 上的不动点个数(函数
上的不动点个数(函数![]() 的不动点即为方程
的不动点即为方程![]() 的解).
的解).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】欧拉公式![]() (
(![]() 为虚数单位,
为虚数单位,![]() ,
,![]() 为自然底数)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,
为自然底数)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,![]() 表示的复数在复平面中位于( )
表示的复数在复平面中位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学是研究数量、结构、变化、空间以及信息等概念的一门科学.在人类历史发展和社会生活中,数学发挥着不可替代的作用,也是学习和研究现代科学技术必不可少的基本工具.
(1)为调查大学生喜欢数学命题是否与性别有关,随机选取![]() 名大学生进行问卷调查,当被调查者问卷评分不低于
名大学生进行问卷调查,当被调查者问卷评分不低于![]() 分则认为其喜欢数学命题,当评分低于
分则认为其喜欢数学命题,当评分低于![]() 分则认为其不喜欢数学命题,问卷评分的茎叶图如下:
分则认为其不喜欢数学命题,问卷评分的茎叶图如下:
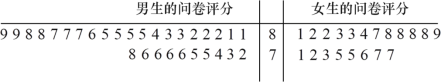
依据上述数据制成如下列联表:
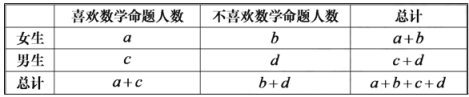
请问是否有![]() 的把握认为大学生是否喜欢数学命题与性别有关?
的把握认为大学生是否喜欢数学命题与性别有关?
参考公式及数据:![]() .
.
|
|
|
|
|
|
|
|
|
|
(2)在某次命题大赛中,![]() 同学要进行
同学要进行![]() 轮命题,其在每轮命题成功的概率均为
轮命题,其在每轮命题成功的概率均为![]() ,各轮命题相互独立,若该同学在
,各轮命题相互独立,若该同学在![]() 轮命题中恰有
轮命题中恰有![]() 次成功的概率为
次成功的概率为![]() ,记该同学在
,记该同学在![]() 轮命题中的成功次数为
轮命题中的成功次数为![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com