
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(厘米) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长y(码) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(厘米) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y(码) | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (I)分别求出$\overline{x}$,$\overline{y}$的值,求出$\widehat{b}$,$\widehat{a}$的值,代入回归方程即可;
(II) 根据高个和大脚的描述,统计出大脚,高个,非大脚和非高个的数据,填入列联表,再在合计的部分填表;
(III)先计算出投掷两次出现情况的总数,再分计算抽到“无效序号(超过20号)”的情况数结合概率的计算公式即可求得抽到“无效序号(超过20号)”的概率.
解答 解:(Ⅰ)“序号为5的倍数”的几组数据:
x1=176,x2=166,x3=168,x4=170,
y1=44,y2=39,y3=40,y4=41,
则$\overline x=170,\overline y=41$,所以$b=\frac{1}{2},a=-44$,
从而y关于x的线性回归方程是$\hat y=\frac{1}{2}x-44$. …(6分)
(Ⅱ)2×2列联表:
| 高 个 | 非高个 | 合计 | |
| 大脚 | 5 | 2 | 7 |
| 非大脚 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
点评 本题考查独立性检验,包括数据的统计,是一个中档题,本题在个别省份作为高考题目出现过,要引起同学们注意.


科目:高中数学 来源: 题型:解答题
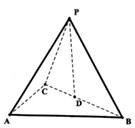 如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.
如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或4 | B. | 1或4 | C. | 1或2 | D. | -6或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±1 | B. | ±2 | C. | $±\sqrt{2}$ | D. | $±\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
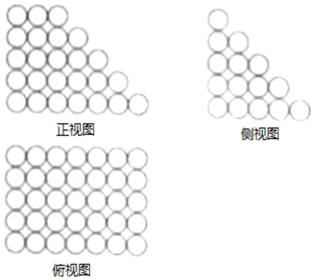 北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}[{({2b+d})a+({b+2d})c}]+\frac{n}{6}({c-a})$.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为85.
北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}[{({2b+d})a+({b+2d})c}]+\frac{n}{6}({c-a})$.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为85.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com