
分析 由已知向量垂直得到数量积为0,由此得到x,y的等式,用,x,y表示|$\overrightarrow{a}+\overrightarrow{b}$|,求最小值.
解答 解:因为向量$\overrightarrow{a}$=(2,1)和$\overrightarrow{b}$=(x-1,y)垂直,所以2x-2+y=0,
所以$\overrightarrow{a}+\overrightarrow{b}$=(x+1,y+1),|$\overrightarrow{a}+\overrightarrow{b}$|2=(x+1)2+(y+1)2,|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{(x+1)^{2}+(y+1)^{2}}$表示(-1,-1)到直线上点的距离,
所以|$\overrightarrow{a}+\overrightarrow{b}$|的最小值为$\frac{|-2-2-1|}{\sqrt{5}}=\sqrt{5}$;
故答案为:$\sqrt{5}$.
点评 本题考查了向量垂直的性质以及向量模的求法;本题利用了点到直线的距离求最小值.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三段论推理 | B. | 假言推理 | C. | 关系推理 | D. | 完全归纳推理 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
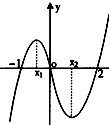
| A. | $\frac{2}{3}$ | B. | $\frac{10}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{28}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 既奇又偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com