
分析 做出图形,根据条件得出△OAC三边的关系,利用余弦定理求出cosA.
解答  解:∵设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,取AB的中点C,则$\overrightarrow{OC}$=$\frac{1}{2}$($\overrightarrow{a}+\overrightarrow{b}$),$\overrightarrow{CA}$=$\frac{1}{2}$($\overrightarrow{a}-\overrightarrow{b}$),
解:∵设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,取AB的中点C,则$\overrightarrow{OC}$=$\frac{1}{2}$($\overrightarrow{a}+\overrightarrow{b}$),$\overrightarrow{CA}$=$\frac{1}{2}$($\overrightarrow{a}-\overrightarrow{b}$),
∵$|{\overrightarrow a}|=\frac{1}{2}|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a-\overrightarrow b}|$,
∴OA=OC=2AC,
∴cosA=$\frac{O{A}^{2}+A{C}^{2}-O{C}^{2}}{2OA•AC}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查了平面向量的数量积运算,平面向量的几何意义,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
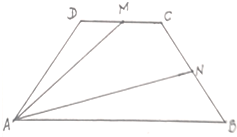 如图,在底角为45°的等腰梯形ABCD中,$\overrightarrow{AB}$=3$\overrightarrow{DC}$,M,N分别为CD,BC的中点.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图,在底角为45°的等腰梯形ABCD中,$\overrightarrow{AB}$=3$\overrightarrow{DC}$,M,N分别为CD,BC的中点.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}{x^2}-5{y^2}=1$ | B. | $5{y^2}-\frac{5}{4}{x^2}=1$ | C. | $5{x^2}-\frac{5}{4}{y^2}=1$ | D. | $\frac{5}{4}{y^2}-5{x^2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 次数(x) | 30 | 33 | 35 | 37 | 39 | 44 | 46 | 50 |
| 成绩(y) | 30 | 34 | 37 | 39 | 42 | 46 | 48 | 51 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com