Question

12．运动员训练次数与运动成绩之间的数据关系如下：

次数（x）	30	33	35	37	39	44	46	50
成绩（y）	30	34	37	39	42	46	48	51

（1）做出散点图；
（2）求出线性回归方程；
（3）做出残差图；
（4）计算R²；
（5）试预测该运动员训练47次及55次的成绩．

Answer 1

分析 （1）根据所给数据，做出散点图；
（2）求出回归系数，求出线性回归方程；
（3）列出运动员训练次数和成绩的原始数据以及相应的残差数据，做出残差图；
（4）计算相关指数R²=0.9855，说明了该运动员的成绩的差异有98.55%是由训练次数引起的．
（5）将x=47和x=55分别代入该方程可得$\stackrel{∧}{y}$=49、$\stackrel{∧}{y}$=57，故预测该运动员训练47次和55次的成绩分别为49和55．

解答 解：（1）做出该运动员训练次数x和与成绩y的散点图，如图所示，由散点图可知，它们之间具有相关关系．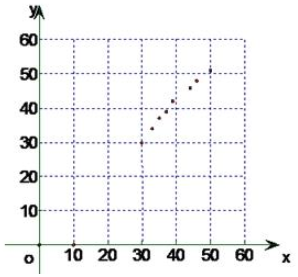

$\overline{x}$=39.25，$\overline{y}$=40.875，$\sum_{i=1}^{8}{{x}_{i}}^{2}$=12656，$\sum_{i=1}^{8}{{y}_{i}}^{2}$=13180，$\sum_{i=1}^{8}{x}_{i}{y}_{i}$=13180，
∴$\stackrel{∧}{b}$≈1.0415，$\stackrel{∧}{a}$=-0.00302，
∴回归直线方程为$\stackrel{∧}{y}$=1.0415x-0.00302．
（3）残差分析：下面的表格列出了运动员训练次数和成绩的原始数据以及相应的残差数据．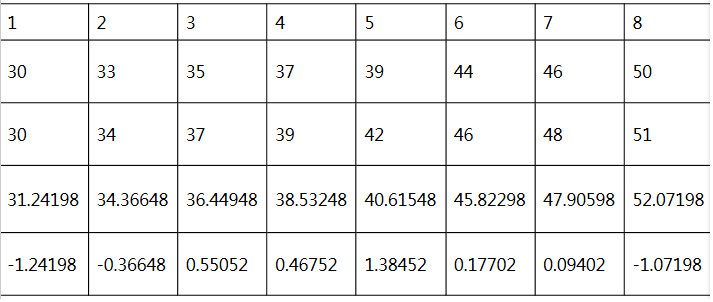

作残差图，如图所示，由图可知，残差点比较均匀地分布在水平带状区域内，说明选择的模型比较合适．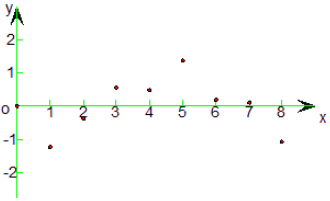

（4）计算相关指数R²=0.9855，说明了该运动员的成绩的差异有98.55%是由训练次数引起的．
（5）做出预报：由上述分析可知，回归直线方程$\stackrel{∧}{y}$=1.0415x-0.00302可以作为该运动员训练成绩的预报值．
将x=47和x=55分别代入该方程可得$\stackrel{∧}{y}$=49、$\stackrel{∧}{y}$=57，故预测该运动员训练47次和55次的成绩分别为49和55．

点评 本题考查回归方程，考查学生利用叔叔知识解决实际问题，属于中档题．