
| A. | $\frac{π}{4}$ | B. | $\frac{1}{2}$ | C. | $1-\frac{π}{4}$ | D. | $\frac{π}{4}-\frac{1}{2}$ |
分析 先利用二项式定理求出k值,再利用圆的面积公式求阴影部分的面积,然后利用几何概型的概率公式解答.
解答 解:根据题意得 ${C}_{k}^{3}•(\frac{1}{k})^{3}$=$\frac{1}{16}$,
解得:k=4或 k=$\frac{4}{5}$(舍去)
解方程组$\left\{\begin{array}{l}{y=\sqrt{8x-{x}^{2}}}\\{y=x}\end{array}\right.$,
解得:x=0或4
∴阴影部分的面积为$\frac{1}{4}π•{4}^{2}-\frac{1}{2}×4×4$=4π-8
任取x∈[0,4],y∈[0,4],则点(x,y)对应 区域面积为4×4=16,
由几何概型概率求法得点(x,y)恰好落在阴影区域内的概率为$\frac{4π-8}{16}$=$\frac{π}{4}-\frac{1}{2}$
故选D.
点评 本题主要考查了二项式定理和几何概型的概率求法,考查学生的计算能力,属于中档题.


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:解答题
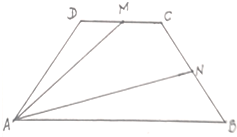 如图,在底角为45°的等腰梯形ABCD中,$\overrightarrow{AB}$=3$\overrightarrow{DC}$,M,N分别为CD,BC的中点.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图,在底角为45°的等腰梯形ABCD中,$\overrightarrow{AB}$=3$\overrightarrow{DC}$,M,N分别为CD,BC的中点.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分但不必要条件 | B. | 充分且必要条件 | ||
| C. | 必要但不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}{x^2}-5{y^2}=1$ | B. | $5{y^2}-\frac{5}{4}{x^2}=1$ | C. | $5{x^2}-\frac{5}{4}{y^2}=1$ | D. | $\frac{5}{4}{y^2}-5{x^2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 次数(x) | 30 | 33 | 35 | 37 | 39 | 44 | 46 | 50 |
| 成绩(y) | 30 | 34 | 37 | 39 | 42 | 46 | 48 | 51 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com