
【题目】已知函数![]() .
.
(1)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)函数![]() 在区间
在区间![]() 上的极值点从小到大分别为
上的极值点从小到大分别为![]() ,证明:
,证明:
(Ⅰ)![]() ;
;
(Ⅱ)对一切![]() 成立.
成立.
【答案】(1)两个零点;(2)(I)见解析;(Ⅱ)见解析
【解析】
(1)对![]() 求导,利用导数得出函数
求导,利用导数得出函数![]() 的单调性,结合零点存在性定理即可得出零点的个数;
的单调性,结合零点存在性定理即可得出零点的个数;
(2) (Ⅰ)对函数![]() 求导,由(1)得出
求导,由(1)得出![]() 的范围,进而得到
的范围,进而得到![]() ,利用诱导公式即可得出
,利用诱导公式即可得出![]() ;
;
(Ⅱ)由(Ⅰ)得出![]() >
>![]() >
>![]() ,结合
,结合![]() 的单调性确定
的单调性确定![]() ,且
,且![]() ,对n为偶数和奇数进行分类讨论,即可得出对一切
,对n为偶数和奇数进行分类讨论,即可得出对一切![]() 成立.
成立.
(1)![]()
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() 在
在![]() 上无零点
上无零点
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]()
![]() 在
在![]() 上有唯一零点
上有唯一零点
当![]() 时,
时,![]() ,
,![]() 上单调递减
上单调递减
![]() ,
,![]() 上有唯一零点
上有唯一零点
综上,函数![]() 在区间
在区间![]() 上有两个零点。
上有两个零点。
(2)![]()
(I)由(1)知![]() 在
在![]() 无极值点;在
无极值点;在![]() 有极小值点,即为
有极小值点,即为![]() ;
;
在![]() 有极大值点,即为
有极大值点,即为![]() ,同理可得,在
,同理可得,在![]() 有极小值点
有极小值点![]() ,
,
在![]() 有极值点
有极值点![]() .由
.由![]() 得
得![]()
![]()
![]()
![]() ,
,![]() ,由函数
,由函数![]() 在
在![]() 单调递增,
单调递增,
得![]() ,
,![]() ,
,
由![]() 在
在![]() 单调递减得
单调递减得![]()
![]()
![]() ;
;
(Ⅱ)同理![]() ,
,![]() >
>![]() >
>![]()
由![]() 在
在![]() 上单调递减得
上单调递减得![]()
![]() ,且
,且![]()
当n为偶数时,从![]() 开始相邻两项配对,每组和均为负值,
开始相邻两项配对,每组和均为负值,
即![]() ,结论成立;
,结论成立;
当n为奇数时,从![]() 开始相邻两项配对,每组和均为负值,还多出最后一项也是负值,即
开始相邻两项配对,每组和均为负值,还多出最后一项也是负值,即![]() ,结论也成立。
,结论也成立。
综上,对一切![]() ,
,![]() 成立.
成立.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 为椭圆
为椭圆![]() (
(![]() )和双曲线
)和双曲线![]() 的公共顶点,
的公共顶点,![]() 、
、![]() 分为双曲线和椭圆上不同于
分为双曲线和椭圆上不同于![]() 、
、![]() 的动点,且满足
的动点,且满足![]() ,设直线
,设直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)求证:点![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)求![]() 的值;
的值;
(3)若![]() 、
、![]() 分别为椭圆和双曲线的右焦点,且
分别为椭圆和双曲线的右焦点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:
①若函数f(x)既是奇函数又是偶函数,则f(x)的值域为{0};
②若函数f(x)是偶函数,则f(|x|)=f(x);
③若函数f(x)在其定义域内不是单调函数,则f(x)不存在反函数;
④若函数f(x)存在反函数f﹣1(x),且f﹣1(x)与f(x)不完全相同,则f(x)与f﹣1(x)图象的公共点必在直线y=x上;
其中真命题的序号是 .(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年3月5日,国务院总理李克强作出的政府工作报告中,提到要“惩戒学术不端,力戒学术不端,力戒浮躁之风”.教育部2014年印发的《学术论文抽检办法》通知中规定:每篇抽检的学术论文送3位同行专家进行评议,3位专家中有2位以上(含3位)专家评议意见为“不合格”的学术论文,将认定为“存在问题学术论文”.有且只有1位专家评议意见为“不合格”的学术论文,将再送另外2位同行专家(不同于前3位专家)进行复评,2位复评专家中有1位以上(含1位)专家评议意见为“不合格”的学术论文,将认定为“存在问题学术论文”.设每篇学术论文被每位专家评议为“不合格”的概率均为![]() ,且各篇学术论文是否被评议为“不合格”相互独立.
,且各篇学术论文是否被评议为“不合格”相互独立.
(1)若![]() ,求抽检一篇学术论文,被认定为“存在问题学术论文”的概率;
,求抽检一篇学术论文,被认定为“存在问题学术论文”的概率;
(2)现拟定每篇抽检论文不需要复评的评审费用为900元,需要复评的总评审费用1500元;若某次评审抽检论文总数为3000篇,求该次评审费用期望的最大值及对应![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数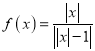 ,给出以下四个命题,其中真命题的序号是_______.
,给出以下四个命题,其中真命题的序号是_______.
①![]() 时,
时,![]() 单调递减且没有最值;
单调递减且没有最值;
②方程![]() 一定有解;
一定有解;
③如果方程![]() 有解,则解的个数一定是偶数;
有解,则解的个数一定是偶数;
④![]() 是偶函数且有最小值.
是偶函数且有最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com