已知函数
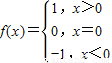
,则函数g(x)=x
2f(x-1)的值域是( )
A.(-∞,+∞)
B.(-1,0)∪[1,+∞)
C.(-∞,0]∪(1,+∞)
D.(-1,+∞)
【答案】
分析:f(x)=

,当x>1时,x-1>0,g(x)=x
2f(x-1)=x
2>1;当x=1时,g(x)=x
2f(x-1)=0;当0<x<1时,g(x)=x
2f(x-1)=-x
2∈(-1,0);当x<0时,g(x)=x
2f(x-1)=-x
2<0.由此能求出函数g(x)=x
2f(x-1)的值域.
解答:解:∵f(x)=

,
∴当x>1时,x-1>0,f(x-1)=1,
g(x)=x
2f(x-1)=x
2>1;
当x=1时,x-1=0,f(x-1)=0,
g(x)=x
2f(x-1)=0;
当0<x<1时,x-1<0,f(x-1)=-1,
g(x)=x
2f(x-1)=-x
2∈(-1,0);
当x<0时,x-1<0,f(x-1)=-1,
g(x)=x
2f(x-1)=-x
2<0.
综上所述,函数g(x)=x
2f(x-1)的值域(-∞,0]∪(1,+∞).
故选C.
点评:本题考查函数的性质和应用,是基础题.解题时要认真审题,仔细解答,注意分类讨论思想的合理运用.
练习册系列答案
相关习题
科目:高中数学
来源:湖南省湖南师大附中2012届高三上学期第一次月考数学文科试题
题型:022
已知函数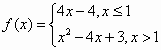 ,则函数g(x)=f(x)-log4x的零点个数为________.
,则函数g(x)=f(x)-log4x的零点个数为________.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖南师大附中高三第一次月考数学试卷(理科)(解析版)
题型:填空题
已知函数
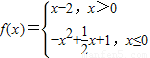
,则函数g(x)=f(x)+x的零点的个数是
个.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖南省湘西州泸溪一中高三(上)期中数学试卷(理科)(解析版)
题型:选择题
已知函数
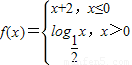
,则函数g(x)=f(x)-x的零点有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学
来源:2010年北京市首师大附中高三大练习数学试卷08(文科)(解析版)
题型:填空题
已知函数

,则函数g(x)=f(x)-2的零点是
.
查看答案和解析>>

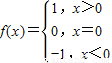 ,则函数g(x)=x2f(x-1)的值域是( )
,则函数g(x)=x2f(x-1)的值域是( ) ,当x>1时,x-1>0,g(x)=x2f(x-1)=x2>1;当x=1时,g(x)=x2f(x-1)=0;当0<x<1时,g(x)=x2f(x-1)=-x2∈(-1,0);当x<0时,g(x)=x2f(x-1)=-x2<0.由此能求出函数g(x)=x2f(x-1)的值域.
,当x>1时,x-1>0,g(x)=x2f(x-1)=x2>1;当x=1时,g(x)=x2f(x-1)=0;当0<x<1时,g(x)=x2f(x-1)=-x2∈(-1,0);当x<0时,g(x)=x2f(x-1)=-x2<0.由此能求出函数g(x)=x2f(x-1)的值域. ,
,

 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案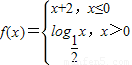 ,则函数g(x)=f(x)-x的零点有( )
,则函数g(x)=f(x)-x的零点有( )