
 (2012•湖北模拟)某地兴建一休闲商业广场,欲在如图所示的一块不规则用地规划建成一个矩形的商业楼区,余下作为休闲区域,已知AB⊥BC,OA∥BC,且AB=BC=2AO=4km,曲线段OC是以O为顶点且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在AB、BC上,且一个顶点落在曲线段OC上,应如何规划才能使矩形商业楼区的用地面积最大?
(2012•湖北模拟)某地兴建一休闲商业广场,欲在如图所示的一块不规则用地规划建成一个矩形的商业楼区,余下作为休闲区域,已知AB⊥BC,OA∥BC,且AB=BC=2AO=4km,曲线段OC是以O为顶点且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在AB、BC上,且一个顶点落在曲线段OC上,应如何规划才能使矩形商业楼区的用地面积最大?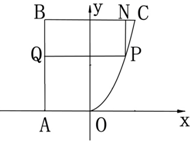 如图,以O为原点,OA所在直线为x轴,建立直角坐标系,则C(2,4)
如图,以O为原点,OA所在直线为x轴,建立直角坐标系,则C(2,4)| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 32 |
| 9 |
| 32 |
| 9 |
| 8 |
| 3 |


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
| RM |
| MQ |
| RN |
| NQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•湖北模拟)已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<π)个单位得到,这两个函数的部分图象如图所示,则φ=
(2012•湖北模拟)已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<π)个单位得到,这两个函数的部分图象如图所示,则φ=| π |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-m |
| f(x) |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com