【答案】
分析:当x=

π 时,函数值为3sin

π=-3,为最小值,故图象C关于直线x=

π对称,故 ①正确.
当x=

π 时,函数值为 sinπ=0,故图象C关于点(

,0)对称,故②正确.
由 2kπ-
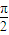
≤2x-

≤2kπ+

,k∈z,可得函数的增区间为(kπ-

,kπ+

),故 ③正确.
由y=3sin2x的图象向右平移

个单位长度可以得到y=3sin2(x-

)=3sin(2x-
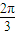
)的图象,故④不正确.
解答:解:对于函数f(x)=3sin(2x-

),当x=

π 时,函数值为3sin

π=-3,为最小值,
故图象C关于直线x=

π对称,故 ①正确.
当x=

π 时,函数值为 sinπ=0,故图象C关于点(
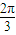
,0)对称,故②正确.
由 2kπ-

≤2x-

≤2kπ+
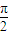
,k∈z,可得 kπ-

≤x≤kπ+
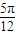
,故函数的增区间为(kπ-
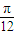
,kπ+
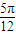
),
故函数f(x)在区间(-

,

)上是增函数,故 ③正确.
由y=3sin2x的图象向右平移

个单位长度可以得到y=3sin2(x-
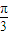
)=3sin(2x-

)的图象,故④不正确.
故只有 ①②③正确,
故选 C.
点评:本题考查正弦函数的对称性,函数y=Asin(ωx+∅)的图象变换,掌握函数y=Asin(ωx+∅)的图象性质,是解题的
关键.

 )的图象为C,给出四个结论:
)的图象为C,给出四个结论: π对称;
π对称; ,0)对称;
,0)对称;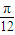 ,
,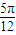 )上是增函数;
)上是增函数;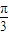 个单位长度可以得到图象C.
个单位长度可以得到图象C. π 时,函数值为3sin
π 时,函数值为3sin π=-3,为最小值,故图象C关于直线x=
π=-3,为最小值,故图象C关于直线x= π对称,故 ①正确.
π对称,故 ①正确. π 时,函数值为 sinπ=0,故图象C关于点(
π 时,函数值为 sinπ=0,故图象C关于点( ,0)对称,故②正确.
,0)对称,故②正确.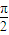 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,可得函数的增区间为(kπ-
,k∈z,可得函数的增区间为(kπ- ,kπ+
,kπ+ ),故 ③正确.
),故 ③正确. 个单位长度可以得到y=3sin2(x-
个单位长度可以得到y=3sin2(x- )=3sin(2x-
)=3sin(2x-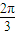 )的图象,故④不正确.
)的图象,故④不正确. ),当x=
),当x= π 时,函数值为3sin
π 时,函数值为3sin π=-3,为最小值,
π=-3,为最小值, π对称,故 ①正确.
π对称,故 ①正确. π 时,函数值为 sinπ=0,故图象C关于点(
π 时,函数值为 sinπ=0,故图象C关于点(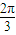 ,0)对称,故②正确.
,0)对称,故②正确. ≤2x-
≤2x- ≤2kπ+
≤2kπ+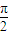 ,k∈z,可得 kπ-
,k∈z,可得 kπ- ≤x≤kπ+
≤x≤kπ+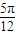 ,故函数的增区间为(kπ-
,故函数的增区间为(kπ-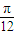 ,kπ+
,kπ+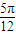 ),
), ,
, )上是增函数,故 ③正确.
)上是增函数,故 ③正确. 个单位长度可以得到y=3sin2(x-
个单位长度可以得到y=3sin2(x-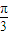 )=3sin(2x-
)=3sin(2x- )的图象,故④不正确.
)的图象,故④不正确.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案