
【题目】已知有穷数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .若数列
.若数列![]() 中各项都是集合
中各项都是集合![]() 的元素,则称该数列为
的元素,则称该数列为![]() 数列.对于
数列.对于![]() 数列
数列![]() ,定义如下操作过程
,定义如下操作过程![]() :从
:从![]() 中任取两项
中任取两项![]() ,
,![]() ,将
,将![]() 的值添在
的值添在![]() 的最后,然后删除
的最后,然后删除![]() ,
,![]() ,这样得到一个
,这样得到一个![]() 项的新数列
项的新数列![]() (约定:一个数也视作数列).若
(约定:一个数也视作数列).若![]() 还是
还是![]() 数列,可继续实施操作过程
数列,可继续实施操作过程![]() ,得到的新数列记作
,得到的新数列记作![]() ,
,![]() ,如此经过
,如此经过![]() 次操作后得到的新数列记作
次操作后得到的新数列记作![]() .
.
(1)设![]() ,
,![]() ,
,![]() 请写出
请写出![]() 的所有可能的结果;
的所有可能的结果;
(2)求证:对于一个![]() 项的
项的![]() 数列
数列![]() 操作
操作![]() 总可以进行
总可以进行![]() 次;
次;
(3)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 求
求![]() 的可能结果,并说明理由.
的可能结果,并说明理由.
【答案】(1)![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() .;(2)证明见解析;(3)
.;(2)证明见解析;(3)![]()
【解析】
(1)直接按定义来操作,每次取两个数代入计算即可求出![]() 的所有可能的结果;
的所有可能的结果;
(2)先通过作差得到每次操作后新数列仍是![]() 数列;再根据每次操作中都是增加一项,删除两项即可得到结论;
数列;再根据每次操作中都是增加一项,删除两项即可得到结论;
(3)先定义运算:![]() ,并证明这种运算满足交换律和结合律;再结合(2)可知
,并证明这种运算满足交换律和结合律;再结合(2)可知![]() 中仅有一项,再按定义先求出
中仅有一项,再按定义先求出![]() ,综合即可得到
,综合即可得到![]() 的可能结果.
的可能结果.
(1)直接按定义来操作,当取0,![]() 时代入计算可得:
时代入计算可得:![]() ,
,![]() ;
;
当取0,![]() 时可得
时可得![]() ,
,![]() ;
;
当取![]() ,
,![]() 时,可得
时,可得![]() ,
,![]() .
.
故有如下的三种可能结果:![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() .
.
(2)因为对![]() ,
,![]() ,有
,有
![]() 且
且![]()
所以![]() ,即每次操作后新数列仍是
,即每次操作后新数列仍是![]() 数列.
数列.
又由于每次操作中都是增加一项,删除两项,
所以对![]() 数列
数列![]() 每操作一次,项数就减少一项,
每操作一次,项数就减少一项,
所以对![]() 项的
项的![]() 数列
数列![]() 可进行
可进行![]() 次操作(最后只剩下一项).
次操作(最后只剩下一项).
(3)由(2)可知![]() 中仅有一项.
中仅有一项.
对于满足![]() ,
,![]() 的实数
的实数![]() ,
,![]() 定义运算:
定义运算:![]() ,
,
下面证明这种运算满足交换律和结合律.
因为![]() ,且
,且![]() ,所以
,所以![]() ,即该运算满足交换律;
,即该运算满足交换律;
因为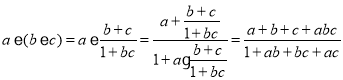
且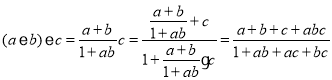
所以![]() ,即该运算满足结合律.
,即该运算满足结合律.
所以![]() 中的项与实施的具体操作过程无关,
中的项与实施的具体操作过程无关,
选择如下操作过程求![]()
由(1)可知![]() ;
;
易知![]() ,
,![]() ,
,![]() ,
,![]() ;
;
所以![]() ,0,0,0,0;
,0,0,0,0;
易知![]() 经过4次操作后剩下一项为
经过4次操作后剩下一项为![]() .
.
综上可知:![]() .
.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项积为
项积为![]() ,满足
,满足![]() . 数列
. 数列![]() 的首项为
的首项为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)记集合![]() ,若集合
,若集合![]() 的元素个数为
的元素个数为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]() 使得
使得![]() 成立?如果存在,请写出
成立?如果存在,请写出![]() 满足的条件,如果不存在,请说明理由.
满足的条件,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1、F2分别为椭圆C:![]() =1(a>b>0)的左、右焦点,点A为椭圆C的左顶点,点B为椭圆C的上顶点,且|AB|=
=1(a>b>0)的左、右焦点,点A为椭圆C的左顶点,点B为椭圆C的上顶点,且|AB|=![]() ,△BF1F2为直角三角形.
,△BF1F2为直角三角形.
(1)求椭圆C的方程;
(2)设直线y=kx+2与椭圆交于P、Q两点,且OP⊥OQ,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将向量![]() =(
=(![]() ,
, ![]() ),
), ![]() =(
=(![]() ,
, ![]() ),…
),…![]() =(
=(![]() ,
,![]() )组成的系列称为向量列{
)组成的系列称为向量列{![]() },并定义向量列{
},并定义向量列{![]() }的前
}的前![]() 项和
项和![]() .如果一个向量列从第二项起,每一项与前一项的差都等于同一个向量,那么称这样的向量列为等差向量列。若向量列{
.如果一个向量列从第二项起,每一项与前一项的差都等于同一个向量,那么称这样的向量列为等差向量列。若向量列{![]() }是等差向量列,那么下述四个向量中,与
}是等差向量列,那么下述四个向量中,与![]() 一定平行的向量是 ( )
一定平行的向量是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,当
,当![]() 时,满足
时,满足![]() .
.
(1)求证:![]() ;
;
(2)求证:数列![]() 为等差数列;
为等差数列;
(3)若![]() ,公差
,公差![]() ,问是否存在
,问是否存在![]() ,
,![]() ,使得
,使得![]() ?如果存在,求出所有满足条件的
?如果存在,求出所有满足条件的![]() ,
,![]() ,如果不在,请说明理由.
,如果不在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD//BC,BC=2AD,AD⊥CD,PD⊥平面ABCD,E为PB的中点.
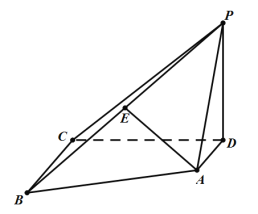
(1)求证:AE//平面PDC;
(2)若BC=CD=PD,求直线AC与平面PBC所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com