
【题目】设F1、F2分别为椭圆C:![]() =1(a>b>0)的左、右焦点,点A为椭圆C的左顶点,点B为椭圆C的上顶点,且|AB|=
=1(a>b>0)的左、右焦点,点A为椭圆C的左顶点,点B为椭圆C的上顶点,且|AB|=![]() ,△BF1F2为直角三角形.
,△BF1F2为直角三角形.
(1)求椭圆C的方程;
(2)设直线y=kx+2与椭圆交于P、Q两点,且OP⊥OQ,求实数k的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用勾股定理a2+b2=3,利用焦点三角形为直角三角形可知b=c,结合b2+c2=a2可求出![]() ,进而可得椭圆C的方程;
,进而可得椭圆C的方程;
(2)联立直线与椭圆方程,可得关于x的一元二次方程,利用直线与椭圆有交点可知![]() ,结合韦达定理及OP⊥OQ,转化为向量数量积为零,计算即得结论.
,结合韦达定理及OP⊥OQ,转化为向量数量积为零,计算即得结论.
(1)由题可知![]() ,所以a2+b2=3,因为△BF1F2为直角三角形,所以b=c,
,所以a2+b2=3,因为△BF1F2为直角三角形,所以b=c,
又b2+c2=a2,所以![]() ,所以椭圆方程为:
,所以椭圆方程为:![]() .
.
(2)由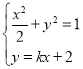 ,得:(1+2k2)x2+8kx+6=0,
,得:(1+2k2)x2+8kx+6=0,
由△=(8k)2﹣4(1+2k2)6>0,得:![]() ,
,
设P(x1,y1),Q(x2,y2),则有![]() ,
,
因为OP⊥OQ,所以![]()
=![]() ,
,
所以k2=5,满足![]() ,所以
,所以![]() .
.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】某区在2019年教师招聘考试中,参加![]() 、
、![]() 、
、![]() 、
、![]() 四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
岗位 | 男性应聘人数 | 男性录用人数 | 男性录用比例 | 女性应聘人数 | 女性录用人数 | 女性录用比例 |
| 269 | 167 | 62% | 40 | 24 | 60% |
| 217 | 69 | 32% | 386 | 121 | 31% |
| 44 | 26 | 59% | 38 | 22 | 58% |
| 3 | 2 | 67% | 3 | 2 | 67% |
总计 | 533 | 264 | 50% | 467 | 169 | 36% |
(1)从表中所有应聘人员中随机抽取1人,试估计此人被录用的概率;
(2)将应聘![]() 岗位的男性教师记为
岗位的男性教师记为![]() ,女性教师记为
,女性教师记为![]() ,现从应聘
,现从应聘![]() 岗位的6人中随机抽取2人.
岗位的6人中随机抽取2人.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2人性别不同”,求事件
为事件“抽取的2人性别不同”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() .
.
(1)证明:数列![]() 为等差数列;
为等差数列;
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,且对任意的正整数n,都有
,且对任意的正整数n,都有![]() ,求整数
,求整数![]() 的值;
的值;
(3)设数列![]() 满足
满足![]() ,若
,若![]() ,且存在正整数s,t,使得
,且存在正整数s,t,使得![]() 是整数,求
是整数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有穷数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .若数列
.若数列![]() 中各项都是集合
中各项都是集合![]() 的元素,则称该数列为
的元素,则称该数列为![]() 数列.对于
数列.对于![]() 数列
数列![]() ,定义如下操作过程
,定义如下操作过程![]() :从
:从![]() 中任取两项
中任取两项![]() ,
,![]() ,将
,将![]() 的值添在
的值添在![]() 的最后,然后删除
的最后,然后删除![]() ,
,![]() ,这样得到一个
,这样得到一个![]() 项的新数列
项的新数列![]() (约定:一个数也视作数列).若
(约定:一个数也视作数列).若![]() 还是
还是![]() 数列,可继续实施操作过程
数列,可继续实施操作过程![]() ,得到的新数列记作
,得到的新数列记作![]() ,
,![]() ,如此经过
,如此经过![]() 次操作后得到的新数列记作
次操作后得到的新数列记作![]() .
.
(1)设![]() ,
,![]() ,
,![]() 请写出
请写出![]() 的所有可能的结果;
的所有可能的结果;
(2)求证:对于一个![]() 项的
项的![]() 数列
数列![]() 操作
操作![]() 总可以进行
总可以进行![]() 次;
次;
(3)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 求
求![]() 的可能结果,并说明理由.
的可能结果,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某烘焙店加工一个成本为60元的蛋糕,然后以每个120元的价格出售,如果当天卖不完,剩下的这种蛋糕作餐厨垃圾处理.
(1)若烘焙店一天加工16个这种蛋糕,,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)烘焙店记录了100天这种蛋糕的日需求量(单位:个),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①若烘焙店一天加工16个这种蛋糕,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列与数学期望及方差;
的分布列与数学期望及方差;
②若烘焙店一天加工16个或17个这种蛋糕,仅从获得利润大的角度考虑,你认为应加工16个还是17个?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代计时器的发明时间不晚于战国时代(公元前476年~前222年),其中沙漏就是古代利用机械原理设计的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道流到下部容器,如图,某沙漏由上、下两个圆锥容器组成,圆锥的底面圆的直径和高均为8 cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
(细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
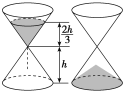
A.2 cmB.![]() cmC.
cmC.![]() cmD.
cmD.![]() cm
cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正东方向,且与
的正东方向,且与![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ,一架飞机从城市
,一架飞机从城市![]() 出发以
出发以![]() 的速度向城市
的速度向城市![]() 飞行,飞行了
飞行,飞行了![]() ,接到命令改变航向,飞向城市
,接到命令改变航向,飞向城市![]() ,此时飞机距离城市
,此时飞机距离城市![]() 有( )
有( )
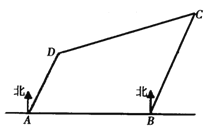
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com