
| A. | 若a>b,c>d,则ab>cd | B. | 若$\frac{1}{a}$>$\frac{1}{b}$,则a<b | ||
| C. | 若a>b,则a2>b2 | D. | 若|a|<b,则a+b>0 |
分析 利用特殊值代入法排除A、B、C,利用不等式的基本性质b-|a|>0,可得 b>±a,从而得到 a+b>0,从而得出结论.
解答 解:对于①,不妨令a=-1,b=-2,c=4,d=1,尽管满足a>b,c>d,但显然不满足ab>cd,故排除A;
对于②,不妨令a=1,b=-1,显然满足$\frac{1}{a}$>$\frac{1}{b}$,但不满足a<b,故排除B;
对于③,不妨令a=-1,b=-2,显然满足a>b,但不满足 a2>b2,故排除C;
对于④,若|a|<b,则b-|a|>0,即 b>±a,∴a+b>0,故D正确,
故选:D.
点评 本题主要考查不等式与不等关系,在限定条件下,比较几个式子的大小,可用特殊值代入法,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| x | 2.00 | 2.20 | 2.60 | 3.20 | 3.40 | 4.00 |
| y | 0.22 | 0.20 | 0.30 | 0.48 | 0.56 | 0.60 |
| $\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}$ | y=a+bx | y=c+dlgx |
| $\sum_{i=1}^{6}({y}_{i}-\stackrel{∧}{{y}_{i}})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-\stackrel{∧}{{y}_{i}})^{2}$ | |
| 0.15 | 0.13 | 0.01 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{2}$-$\frac{\sqrt{3}}{4}$ | D. | $\frac{1}{2}$+$\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ②③ | C. | ①② | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
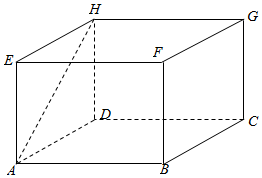 如图所示,长方体ABCD-EFGH,底面是边长为2$\sqrt{3}$的正方形,DH=2,P为AH中点.
如图所示,长方体ABCD-EFGH,底面是边长为2$\sqrt{3}$的正方形,DH=2,P为AH中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com