
分析 设AB=x,在△ABD中由条件和余弦定理求出AB和cos∠BDA,由∠ADB+∠ADC=π和诱导公式求出cos∠CDA,由平方关系求出sin∠ADC,根据内角和定理、∠DAC=$\frac{π}{3}$和两角和的正弦公式求出sin∠C,在△ADC中由正弦定理求出CD的长.
解答 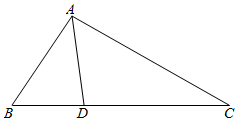 解:如图所示:设AB=x,在△ABD中,∠B=$\frac{π}{3}$,BD=2,AD=2$\sqrt{7}$,
解:如图所示:设AB=x,在△ABD中,∠B=$\frac{π}{3}$,BD=2,AD=2$\sqrt{7}$,
则由余弦定理得,AD2=AB2+BD2-2•AB•BD•cosB
∴28=${x}^{2}+4-2×x×2×\frac{1}{2}$,则x2-2x-24=0,
解得x=6或x=-4(舍去),
cos∠BDA=$\frac{{BD}^{2}+A{D}^{2}-{AB}^{2}}{2•BD•AD}$=$\frac{4+28-36}{2×2×2\sqrt{7}}$=-$\frac{1}{2\sqrt{7}}$
∵∠ADB+∠ADC=π,∴cos∠CDA=-cos∠BDA=$\frac{1}{2\sqrt{7}}$,
则sin∠ADC=$\sqrt{1-co{s}^{2}∠ADC}$=$\frac{3\sqrt{3}}{2\sqrt{7}}$,
∵∠DAC=$\frac{π}{3}$,
∴sin∠C=sin(∠DAC+∠ADC)=sin∠DACcos∠ADC+cos∠DACsin∠ADC
=$\frac{\sqrt{3}}{2}×\frac{1}{2\sqrt{7}}+\frac{1}{2}×\frac{3\sqrt{3}}{2\sqrt{7}}$=$\frac{\sqrt{3}}{\sqrt{7}}$
在△ADC中,由正弦定理得$\frac{AD}{sin∠C}=\frac{CD}{sin∠DAC}$,
∴CD=$\frac{AD•sin∠DAC}{sin∠C}$=$\frac{2\sqrt{7}×\frac{\sqrt{3}}{2}}{\frac{\sqrt{3}}{\sqrt{7}}}$=7,
故答案为:7.
点评 本题考查正弦定理、余弦定理,诱导公式、两角和的正弦公式等应用,熟练掌握公式和定理是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,c>d,则ab>cd | B. | 若$\frac{1}{a}$>$\frac{1}{b}$,则a<b | ||
| C. | 若a>b,则a2>b2 | D. | 若|a|<b,则a+b>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y=0 | B. | y=x | C. | $\sqrt{3}$x-y=0 | D. | $\sqrt{2}x$+y=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com