
【题目】解答
(1)已知全集U={x|﹣5≤x≤10,x∈Z},集合M={x|0≤x≤7,x∈Z},N={x|﹣2≤x<4,x∈Z},求(UN)∩M(分别用描述法和列举法表示结果)
(2)已知全集U=A∪B={0,1,2,3,4,5,6,7,8,9,10},若集合A∩UB={2,4,6,8},求集合B;
(3)已知集合P={x|ax2+2ax+1=0,a∈R,x∈R},当集合P只有一个元素时,求实数a的值,并求出这个元素.
【答案】
(1)
解:由U={x|﹣5≤x≤10,x∈Z},N={x|﹣2≤x<4,x∈Z},
得:CUN={x|﹣5≤x<﹣2或4≤x≤10,x∈Z},
由M={x|0≤x≤7,x∈N},
得(CUN)∩M={x|4≤x≤7,x∈N}={4,5,6,7}
(2)
解:U=A∪B={0,1,2,3,4,5,6,7,8,9,10}
由A∩UB={2,4,6,8},知UB={2,4,6,8},
所以,B={0,1,3,5,7,9,10}
(3)
解:当a=0时,P=;
当a≠0时,△=4a2﹣4a=0集合P只有一个元素
此时a=1,
集合P中的元素为﹣1
【解析】(1)根据补集的定义求出(UN)再根据交集的定义即可求出答案.(2)根据补集的定义即可求出,(3)根据元素和集合的关系即可求出.
【考点精析】掌握集合的表示方法-特定字母法和交、并、补集的混合运算是解答本题的根本,需要知道①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.③描述法:{![]() |
|![]() 具有的性质},其中
具有的性质},其中![]() 为集合的代表元素.④图示法:用数轴或韦恩图来表示集合;求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.
为集合的代表元素.④图示法:用数轴或韦恩图来表示集合;求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=|ax+1|(a∈R),不等式f(x)≤3的解集为{x|﹣2≤x≤1}. (Ⅰ)求a的值;
(Ⅱ)若f(x)﹣2f( ![]() )≤k恒成立,求k的取值范围.
)≤k恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,直线
,直线![]() :
: ![]() ,椭圆
,椭圆![]() :
: ![]() ,
, ![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点.
的左、右焦点.
(1)当直线![]() 过右焦点
过右焦点![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() ,
, ![]() 的重心分别为
的重心分别为![]() ,
, ![]() ,若原点
,若原点![]() 在以线段
在以线段![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,记
,记![]() ,若数列
,若数列![]() 满足:“存在
满足:“存在![]() ,使得只要
,使得只要![]() (
(![]() 且
且![]() ),必有
),必有![]() ”,则称数列
”,则称数列![]() 具有性质
具有性质![]() .
.
(Ⅰ)若数列![]() 满足
满足![]() 判断数列
判断数列![]() 是否具有性质
是否具有性质![]() ?是否具有性质
?是否具有性质![]() ?
?
(Ⅱ)求证:“![]() 是有限集”是“数列
是有限集”是“数列![]() 具有性质
具有性质![]() ”的必要不充分条件;
”的必要不充分条件;
(Ⅲ)已知![]() 是各项为正整数的数列,且
是各项为正整数的数列,且![]() 既具有性质
既具有性质![]() ,又具有性质
,又具有性质![]() ,求证:存在整数
,求证:存在整数![]() ,使得
,使得![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
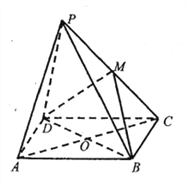
【题目】如图,点![]() 是菱形
是菱形![]() 所在平面外一点,
所在平面外一点, ![]() ,
, ![]() 是等边三角形,
是等边三角形, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 的所成角的大小.
的所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
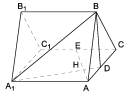
【题目】如图,正三棱柱![]() 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是![]() 棱的中点,AE交
棱的中点,AE交![]() 于点H.
于点H.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,
为矩形, ![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为线段
为线段![]() 中点.
中点.

(Ⅰ)求异面直线![]() 与
与![]() 所成的角的正切值;
所成的角的正切值;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com