
【题目】己知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,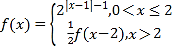 ,则函数
,则函数![]() 在
在![]() 上的所有零点之和为( )
上的所有零点之和为( )
A.7B.8C.9D.10
【答案】B
【解析】
由已知可分析出函数![]() 是偶函数,则其零点必然关于原点对称,故
是偶函数,则其零点必然关于原点对称,故![]() 在
在![]() 上所有的零点的和为
上所有的零点的和为![]() ,则函数
,则函数![]() 在
在![]() 上所有的零点的和,即函数
上所有的零点的和,即函数![]() 在
在![]() 上所有的零点之和,求出
上所有的零点之和,求出![]() 上所有零点,可得答案.
上所有零点,可得答案.
解:![]() 函数
函数![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,![]() .
.
又![]() 函数
函数![]() ,
,
![]() ,
,
![]() 函数
函数![]() 是偶函数,
是偶函数,
![]() 函数
函数![]() 的零点都是以相反数的形式成对出现的.
的零点都是以相反数的形式成对出现的.
![]() 函数
函数![]() 在
在![]() 上所有的零点的和为
上所有的零点的和为![]() ,
,
![]() 函数
函数![]() 在
在![]() 上所有的零点的和,即函数
上所有的零点的和,即函数![]() 在
在![]() 上所有的零点之和.
上所有的零点之和.
由![]() 时,
时,![]() ,
,
即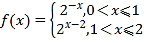
![]() 函数
函数![]() 在
在![]() 上的值域为
上的值域为![]() ,当且仅当
,当且仅当![]() 时,
时,![]()
又![]() 当
当![]() 时,
时,![]()
![]() 函数
函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
函数![]() 在
在![]() 上的值域为
上的值域为![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ,
,
函数![]() 在
在![]() 上的值域为
上的值域为![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 上恒成立,
上恒成立,![]() 在
在![]() 上无零点,
上无零点,
同理![]() 在
在![]() 上无零点,
上无零点,
依此类推,函数![]() 在
在![]() 无零点,
无零点,
综上函数![]() 在
在![]() 上的所有零点之和为8
上的所有零点之和为8
故选:![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按![]() /次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第 | 第 | 第 | 第 |
|
收费比率 |
|
|
|
|
|
该公司注册的会员中没有消费超过![]() 次的,从注册的会员中,随机抽取了100位进行统计,得到统计数据如下:
次的,从注册的会员中,随机抽取了100位进行统计,得到统计数据如下:
消费次数 |
|
|
|
|
|
人数 |
|
|
|
|
|
假设汽车美容一次,公司成本为![]() 元,根据所给数据,解答下列问题:
元,根据所给数据,解答下列问题:
(1)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(2)以事件发生的频率作为相应事件发生的概率,设该公司为一位会员服务的平均利润为![]() 元,求
元,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 经过点
经过点![]() ,且与极轴所成的角为
,且与极轴所成的角为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB=2,BC=1,E是CD的中点,将三角形ADE沿AE翻折到图②的位置,使得平面AED′⊥平面ABC.
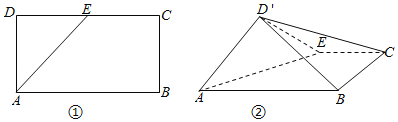
(1)在线段BD'上确定点F,使得CF∥平面AED',并证明;
(2)求△AED'与△BCD'所在平面构成的锐二面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高三年级100名学生的视力情况进行统计(如果两眼视力不同,取较低者统计),得到如图所示的频率分布直方图,已知从这100人中随机抽取1人,其视力在![]() 的概率为
的概率为![]() .
.
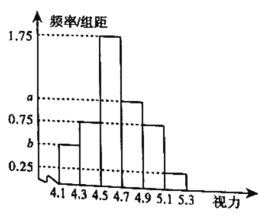
(1)求a,b的值;
(2)若报考高校A专业的资格为:任何一眼裸眼视力不低于5.0,已知在![]() 中有
中有![]() 的学生裸眼视力不低于5.0.现用分层抽样的方法从
的学生裸眼视力不低于5.0.现用分层抽样的方法从![]() 和
和![]() 中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购已经成为一种新型的购物方式,2018年天猫双11,仅1小时47分钟成交额超过1000亿元,比2017年达到1000亿元的时间缩短了7个小时,为了研究市民对网购的依赖性,从A城市16﹣59岁人群中抽取一个容量为100的样本,得出下列2×2列联表,其中16﹣39岁为青年,40﹣59岁为中年,当日消费金额超过1000元为消费依赖网购,否则为消费不依赖网购.
依赖网购 | 不依赖网购 | 小计 | |
青年(16﹣39岁) | 40 | 20 | |
中年(40﹣59岁) | 20 | 20 | |
小计 |
(1)完成2×2列联表,计算X2值,并判断是否有95%的把握认为网购依赖和年龄有关?
(2)把样本中的频率当作概率,随机从A城市中选取5人,其中依赖网购的人数为随机变量X,求随机变量X的分布列及期望(附:X2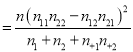 ,当X2>3.841时,有95%的把握说事件A与B有关,当X2≤3.841时,没有95%的把握说事件A与B有关)
,当X2>3.841时,有95%的把握说事件A与B有关,当X2≤3.841时,没有95%的把握说事件A与B有关)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com