
【题目】如图①,在矩形ABCD中,AB=2,BC=1,E是CD的中点,将三角形ADE沿AE翻折到图②的位置,使得平面AED′⊥平面ABC.
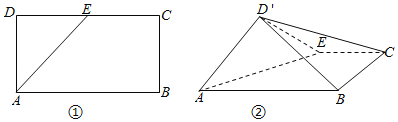
(1)在线段BD'上确定点F,使得CF∥平面AED',并证明;
(2)求△AED'与△BCD'所在平面构成的锐二面角的正切值.
【答案】(1)点F是线段BD'的中点,见解析(2)![]() .
.
【解析】
(1)取BD'的中点![]() ,记AE,BC延长线交于点M,由平面几何知识可得点C是BM的中点,可得CF∥MD',可得CF∥平面AED';
,记AE,BC延长线交于点M,由平面几何知识可得点C是BM的中点,可得CF∥MD',可得CF∥平面AED';
(2)先根据面面垂直的性质可得BE⊥平面AED',在平面AED'内作EN⊥MD',可得∠BNE就是△AED'与△BCD'所在平面构成的锐二面角的平面角,最后解三角形可得锐二面角的正切值.
(1)点F是线段BD'的中点时,CF∥平面AED'.
证明:记AE,BC延长线交于点M,
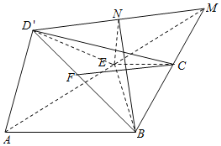
∵AB=2EC,∴点C是BM的中点,
∴CF∥MD',而MD'在平面AED'内,CF在平面AED'外,
∴CF∥平面AED';
(2)在矩形ABCD中,AB=2,CD=1,BE⊥AE,
∵平面AED'⊥平面ABC,且交线是AE,∴BE⊥平面AED',
在平面AED'内作EN⊥MD',连接BN,则BN⊥MD′.
∴∠BNE就是△AED'与△BCD'所在平面构成的锐二面角的平面角,
求解三角形可得![]() ,
,![]() ,
,
∴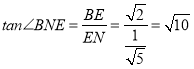 .
.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,抛物线
,抛物线![]() 与圆
与圆![]() 的相交弦长为4.
的相交弦长为4.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)点![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() 为抛物线
为抛物线![]() 上两点,
上两点,![]() ,若
,若![]() 的面积为
的面积为![]() ,且直线
,且直线![]() 的斜率存在,求直线
的斜率存在,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若p∨q为真命题,则p∧q为真命题
B.“x=5”是“x2-4x-5=0”的充分不必要条件
C.命题“若x<-1,则x2-2x-3>0”的否定为:“若x≥-1,则x2-2x-3≤0”
D.已知命题p:x∈R,x2+x-1<0,则![]() p:x∈R,x2+x-1≥0
p:x∈R,x2+x-1≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 将圆
将圆![]() 的圆周分为四等份,且椭圆
的圆周分为四等份,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() 的中点为
的中点为![]() ,线段
,线段![]() 的垂直平分线为
的垂直平分线为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形![]() (边长为2个单位)的顶点
(边长为2个单位)的顶点![]() 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为![]() ,则棋子就按逆时针方向行走
,则棋子就按逆时针方向行走![]() 个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到点
个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到点![]() 处的所有不同走法共有( )
处的所有不同走法共有( )

A. 22种 B. 24种 C. 25种 D. 27种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)
等边△ABC的边长为3,点D,E分别为AB,AC上的点,且满足![]() (如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
(如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
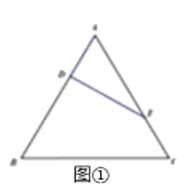
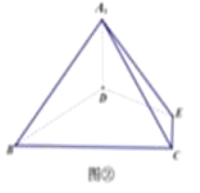
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P(不包括端点),使直线PA1与平面A1BD所成的角为60°?若存在,求出A1P的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于两点
交于两点![]() ,点
,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com