
【题目】椭圆![]() 将圆
将圆![]() 的圆周分为四等份,且椭圆
的圆周分为四等份,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() 的中点为
的中点为![]() ,线段
,线段![]() 的垂直平分线为
的垂直平分线为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知P(3,![]() )是椭圆C:
)是椭圆C:![]() 1
1![]() 上的点,Q是P关于x轴的对称点,椭圆C的离心率为
上的点,Q是P关于x轴的对称点,椭圆C的离心率为![]() .
.
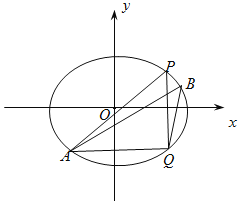
(1)求椭圆C的方程;
(2)A,B是椭圆上位于直线PQ两侧的动点.
①若直线AB的斜率为![]() ,求四边形APBQ面积的最大值.
,求四边形APBQ面积的最大值.
②当A、B在运动过程中满足∠APQ=∠BPQ时,问直线AB的斜率是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双11”促销活动中,某商场为了吸引顾客,搞好促销活动,采用“双色球”定折扣的方式促销,即:在红、黄的两个纸箱中分别装有大小完全相同的红、黄球各5个,每种颜色的5个球上标有1,2,3,4,5等5个数字,顾客结账时,先分别从红、黄的两个纸箱中各取一球,按两个球的数字之和为折扣打折,如![]() ,就按3折付款,并规定取球后不再增加商品.按此规定,顾客享有6折及以下折扣的概率是( )
,就按3折付款,并规定取球后不再增加商品.按此规定,顾客享有6折及以下折扣的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() .
.
(1)令![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:
满足:![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②是否存在正整数![]() ,使得
,使得![]() 成立?若存在,求出所有
成立?若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 经过点
经过点![]() ,且与极轴所成的角为
,且与极轴所成的角为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB=2,BC=1,E是CD的中点,将三角形ADE沿AE翻折到图②的位置,使得平面AED′⊥平面ABC.
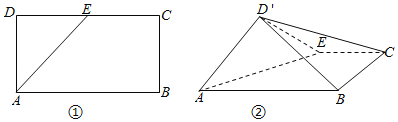
(1)在线段BD'上确定点F,使得CF∥平面AED',并证明;
(2)求△AED'与△BCD'所在平面构成的锐二面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高三年级100名学生的视力情况进行统计(如果两眼视力不同,取较低者统计),得到如图所示的频率分布直方图,已知从这100人中随机抽取1人,其视力在![]() 的概率为
的概率为![]() .
.
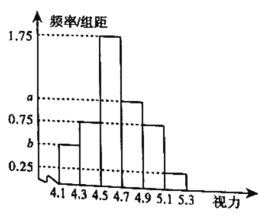
(1)求a,b的值;
(2)若报考高校A专业的资格为:任何一眼裸眼视力不低于5.0,已知在![]() 中有
中有![]() 的学生裸眼视力不低于5.0.现用分层抽样的方法从
的学生裸眼视力不低于5.0.现用分层抽样的方法从![]() 和
和![]() 中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)令![]() ,已知函数
,已知函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,
,
①求实数![]() 的取值范围;
的取值范围;
②若存在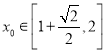 ,使不等式
,使不等式![]() 对任意
对任意![]() (取值范围内的值)恒成立,求实数
(取值范围内的值)恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com