
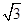 sinωxcosωx+sin2ωx+
sinωxcosωx+sin2ωx+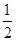 ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为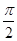 .
.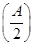 =
=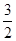 ,求A的值.
,求A的值.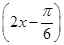 +1;(2)A=
+1;(2)A= 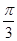 .
. 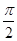 ,得到f(x)的周期为π,利用周期公式求出ω的值.确定出f(x)的解析式.
,得到f(x)的周期为π,利用周期公式求出ω的值.确定出f(x)的解析式.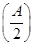 =sin
=sin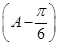 +1=
+1=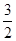 ∴sin
∴sin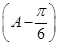 =
=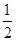 ,再结合A∈(0,π),可得A=
,再结合A∈(0,π),可得A= 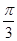 .
.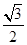 sin2ωx+
sin2ωx+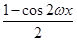 +
+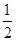
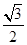 sin2ωx?
sin2ωx?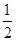 cos2ωx+1=sin
cos2ωx+1=sin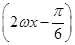 +1
+1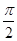 ,∴最小正周期T=π
,∴最小正周期T=π 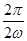 =π,ω=1.
=π,ω=1.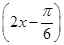 +1
+1 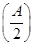 =sin
=sin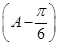 +1=
+1=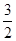 ∴sin
∴sin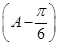 =
=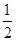
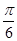 < A?
< A?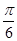 <
< 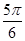
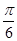 =
= 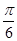 ,故A=
,故A= 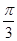 .
. 

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:单选题
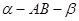 的平面角是锐角,点C
的平面角是锐角,点C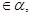 且点C不在棱AB上,D是C在平面
且点C不在棱AB上,D是C在平面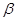 上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )| A.∠CEB>∠DEB | B.∠CEB=∠DEB |
| C.∠CEB<∠DEB | D.∠CEB与∠DEB的大小关系不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com