
【题目】已知椭圆![]() ,过椭圆
,过椭圆![]() 右顶点和上顶点的直线
右顶点和上顶点的直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() (
(![]() ,
,![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在以![]() 为首项,公比为
为首项,公比为![]() (
(![]() ,
,![]() )的数列
)的数列![]() ,
,![]() 使得数列
使得数列![]() 的每一项都是数列
的每一项都是数列![]() 的不同的项,若存在,求出所有满足条件的数列
的不同的项,若存在,求出所有满足条件的数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(请选做其中一题)
(1)请推导等差数列及等比数列前![]() 项和公式;
项和公式;
(2)如果你在海上航行,请设计一种测量海上两个小岛之间距离的方法并作图说明;
(3)某工厂要建造一个长方形无盖贮水池,其容积为4800立方米,深为3米,如果池底每平米的造价为150元,池壁每平米造价为120元,怎样设计水池能使造价最低?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
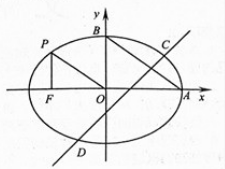
【题目】如图,过椭圆![]() 上一点
上一点![]() 向
向![]() 轴作垂线,垂足为左焦点
轴作垂线,垂足为左焦点![]() ,
,![]() 分别为
分别为![]() 的右顶点,上顶点,且
的右顶点,上顶点,且![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 为
为![]() 上的两点,若四边形
上的两点,若四边形![]()
![]() 逆时针排列)的对角线
逆时针排列)的对角线![]() 所在直线的斜率为
所在直线的斜率为![]() ,求四边形
,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.
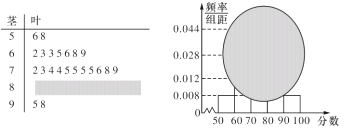
(1)求分数在![]() 的频率及全班人数;
的频率及全班人数;
(2)求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
(3)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为a,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(2)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为![]() ,第二次出现的点数为
,第二次出现的点数为![]() .
.
(1)求事件“![]() ”的概率;
”的概率;
(2)求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com