
 =
= ,
, ×100=8,
×100=8, ×200=16,
×200=16, ×50=4,
×50=4,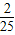 ×150=12,
×150=12,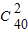 种方法,
种方法, +
+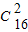 +
+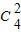 +
+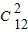 ,
, =
=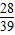 .…(6分)
.…(6分) (k=0,1,2,3)…(9分)
(k=0,1,2,3)…(9分)| P | 1 | 2 | 3 | |
| X | 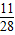 | 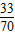 | 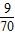 |  |
 +1×
+1× +2×
+2× +3×
+3× =
= …(13分)
…(13分)

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
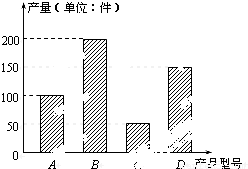
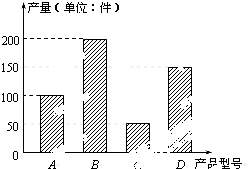 某工厂2013年上半年生产的A,B,C,D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取40件样品参加今年七月份的一个展销会.
某工厂2013年上半年生产的A,B,C,D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取40件样品参加今年七月份的一个展销会.查看答案和解析>>
科目:高中数学 来源: 题型:
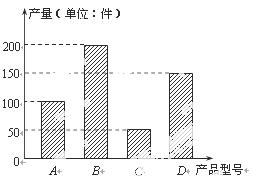
某工厂2013年上半年生产的A,B,C,D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取40件样品参加今年七月份的一个展销会.
(Ⅰ)问:A,B,C,D四种型号的产品分别抽取多少件?
(Ⅱ)从40件样品中随机地抽取2件,求这2件产品恰好是不同型号产品的概率;
(Ⅲ)40件样品中,从C,D型号的产品中随机抽取3件,用X表示抽取的C种型号产品的件数,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com