
【题目】某次测试成绩满分是为150分,设![]() 名学生的得分分别为
名学生的得分分别为![]() ,
,![]() 为
为![]() 名学生中得分至少为
名学生中得分至少为![]() 分的人数.记
分的人数.记![]() 为
为![]() 名学生的平均成绩,则( )
名学生的平均成绩,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】A
【解析】
由于选项中必有一项正确,故本选择题利用特殊法解决.设![]() ,这2名学生的得分分别为150,150.则这2名学生中得分至少为
,这2名学生的得分分别为150,150.则这2名学生中得分至少为![]() 分的人数分别为:2,2,
分的人数分别为:2,2,![]() ,2,2.一共有150个“2”,计算
,2,2.一共有150个“2”,计算![]() 的值,再对照选项即可得到答案.
的值,再对照选项即可得到答案.
利用特殊法解决.
假设![]() ,这2名学生的得分分别为150,150.
,这2名学生的得分分别为150,150.
则这2名学生中得分至少为1分的人数分别为:![]() ,
,
这2名学生中得分至少为2分的人数分别为:![]() ,
,
这2名学生中得分至少为3分的人数分别为:![]() ,
,
![]()
这2名学生中得分至少为150分的人数分别为:![]() ,
,
即这2名学生中得分至少为![]() 分的人数
分的人数![]() 分别为:
分别为:
2,2,![]() ,2,2.一共有150个“2”,
,2,2.一共有150个“2”,
从而得![]() 分的同学会被记
分的同学会被记![]() 次,所有
次,所有![]() 的和恰好是所有人得分的总和,
的和恰好是所有人得分的总和,
即![]() ,
,
从而![]() .
.
![]() .
.
对照选项,只有(A)正确.
故选:![]() .
.


科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元,未售出的产品,每盒亏损
元,未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
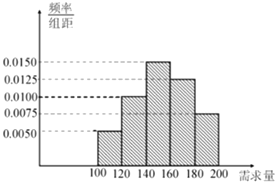
(1)根据直方图估计这个开学季内市场需求量![]() 的众数和平均数(同一组中的数据用该组区间的中点值为代表);
的众数和平均数(同一组中的数据用该组区间的中点值为代表);
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小陈同学进行三次定点投篮测试,已知第一次投篮命中的概率为![]() ,第二次投篮命中的概率为
,第二次投篮命中的概率为![]() ,前两次投篮是否命中相互之间没有影响.第三次投篮受到前两次结果的影响,如果前两次投篮至少命中一次,则第三次投篮命中的概率为
,前两次投篮是否命中相互之间没有影响.第三次投篮受到前两次结果的影响,如果前两次投篮至少命中一次,则第三次投篮命中的概率为![]() ,否则为
,否则为![]() .
.
(1)求小陈同学三次投篮至少命中一次的概率;
(2)记小陈同学三次投篮命中的次数为随机变量![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年冬,北京雾霾天数明显减少,据环保局统计三个月的空气质量,达到优良的天数超过70天.重度污染的天数仅有4天.主要原因是政府对治理雾霾采取了有效措施,如①减少机动车尾气排放;②实施了煤改电或煤改气工程;③关停了大量的排污企业;④部分企业季节性的停产.为了解农村地区实施煤改气工程后天然气使用情况,从某乡镇随机抽取100户,进行均用气量调查,得到的用气量数据(单位:千立方米)均在区间![]() 围内,将数据按区间列表如下:
围内,将数据按区间列表如下:
分组 | 频数 | 频率 |
| 14 | 0.14 |
|
|
|
| 55 | 0.55 |
| 4 | 0.04 |
| 2 | 0.02 |
合计 | 100 | 1 |
(1)求表中![]() ,
,![]() 的值;
的值;
(2)若同组中的每个数据用该组区间中点值代替,估计该乡每户月平均用气量;
(3)从用量高于3千立方米的用户中任选2户,进行燃气使用的满意度调查,求这2户用气量处于不同区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 n 个四元集合 A1 , A2 ,…, An ,每两个有且只有一个公共元 ,并且有Card(A1 ∪ A2 ∪ …∪ An)=n .试求 n 的最大值.这里 Card A 为集合A中元素的个数 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com